Solve the equation 6(2x + 4)² = (2x + 4) +2.
5 9
ОГ
X
4
of
O
X
DONE
5
3
or -
or
Answers
Answer:
x = -9/2 or -5/3
Step-by-step explanation:
The given equation is recognizable as a quadratic in the expression (2x+4). It may be more easily solved by substituting a variable for that expression.
__
setupLet z = 2x+4. Then the equation becomes ...
6z² = z +2
6z^2 -z -2 = 0
solution to the quadraticThis equation can be factored by finding factors of (6)(-2) that total -1.
(6z -4)(6z +3)/6 = 0
(3z -2)(2z +1) = 0 . . . . . eliminate the fraction
The values of z that make these factors zero are ...
3z -2 = 0 ⇒ z = 2/3
2z +1 = 0 ⇒ z = -1/2
values of xThe relation between x and z tells us ...
z = 2x +4
(z -4)/2 = x
For the values of z we have, the corresponding x-values are ...
z = 2/3 ⇒ (2/3 -4)/2 = x = -10/6 = -5/3
z = -1/2 ⇒ (-1/2 -4)/2 = x = -9/4
Solutions to the equation are x=-9/4 and x=-5/3.
_____
Additional comment
Alternatively, the equation could have been expanded to standard form and then factored.
6(4x² +16x +16) = 2x +6
24x² +94x +90 = 0 . . . . put in standard form
12x² +47x +45 = 0 . . . . factor out 2
(4x +9)(3x +5) = 0 . . . . factor (judged harder than the above factoring)
Related Questions
PLEASE HELP! I WILL GIVE BRAINLIST AND THANKS list three physical properties of matter
Answers
Answer:
mean,range,and mode.
I learned this just last Thursday, duh ;)
Step-by-step explanation:
Estimate then find the quotient 2,800÷25
Answers
Answer:
112
Step-by-step explanation:
What is the product
of -5.6 and 12.04?
Answers
the answer to your question is -67.424
A bag contains 10 green,8 blue, and 2 white balls. Naomi seclets 2 balls from the bag at random, one at a time, without replacing them. What is the probability that she selects all two white balls?
E.) 2/95
F.) 1/95
G.) 1/190
H.) 1/380
Answers
To find the probability that Naomi selects both white balls, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total number of outcomes:
Naomi selects 2 balls without replacement, so the total number of outcomes is the number of ways she can choose 2 balls out of the total number of balls in the bag. This can be calculated using combinations:
Total outcomes = C(20, 2) = (20!)/(2!(20-2)!) = (20 * 19)/(2 * 1) = 190
Number of favorable outcomes:
Naomi needs to select 2 white balls. There are 2 white balls in the bag, so the number of favorable outcomes is the number of ways she can choose 2 white balls out of the 2 white balls in the bag:
Favorable outcomes = C(2, 2) = 1
Probability = Favorable outcomes / Total outcomes = 1/190
Therefore, the correct answer is (G) 1/190.
Mr. Gupta gave his students a quiz with three questions on it. Let
�
XX represent the number of questions that a randomly chosen student answered correctly. Here is the probability distribution of
�
XX along with summary statistics:
�
=
# correct
X=# correctX, equals, start text, \#, space, c, o, r, r, e, c, t, end text
0
00
1
11
2
22
3
33
�
(
�
)
P(X)P, left parenthesis, X, right parenthesis
0.05
0.050, point, 05
0.20
0.200, point, 20
0.50
0.500, point, 50
0.25
0.250, point, 25
Mean:
�
�
=
1.95
μ
X
=1.95mu, start subscript, X, end subscript, equals, 1, point, 95
Standard deviation:
�
�
≈
0.8
σ
X
≈0.8sigma, start subscript, X, end subscript, approximately equals, 0, point, 8
Mr. Gupta decides to score the tests by giving
10
1010 points for each correct question. He also plans to give every student
5
55 additional bonus points. Let
�
YY represent a random student's score.
What are the mean and standard deviation of
�
YY?
Answers
The mean score of a random student (YY) is 574.5. the standard deviation of the random student's score (YY) is 8.
How to answer the aforementioned questionGiven:
- Each correct question is worth 10 points.
- Every student receives an additional 555 bonus points.
Let's calculate the mean and standard deviation of YY:
Mean of YY:
The mean score, denoted as μY, can be calculated using the mean of XX (μX) and the scoring scheme:
μY = μX * 10 + 555
Substituting the value of μX from the given information:
μY = 1.95 * 10 + 555
μY = 19.5 + 555
μY = 574.5
Therefore, the mean score of a random student (YY) is 574.5.
Standard Deviation of YY:
The standard deviation of YY, denoted as σY, can be calculated using the standard deviation of XX (σX) and the scoring scheme:
σY = σX * 10
Substituting the value of σX from the given information:
σY = 0.8 * 10
σY = 8
Therefore, the standard deviation of the random student's score (YY) is 8.
Complete question: Mr. Gupta gave his students a quiz with three questions on it. Let X represent the number of questions
that a randomly chosen student answered correctly. Here is the probability distribution of X along with
summary statistics:
0
1
2
2.
3
X = # correct
P(X)
0.05
0.20
0.50
0.25
Mean: Hex = 1.95
Standard deviation: Ox 0.8
Mr. Gupta decides to score the tests by giving 10 points for each correct question. He also plans to give
every student 5 additional bonus points. Let Y represent a random student's score.
What are the mean and standard deviation of Y?
Learn more about standard deviation at https://brainly.com/question/475676
#SPJ1
Tara earned $320 this month and saved $96. Write a ratio statement to describe how much Tara saved versus earned.
Answers
Answer:
3: 10
Step-by-step explanation:
saved: earned
96: 320
simplify by dividing both sides by the same thing just like a fraction:
96: 320
24: 80
6: 20
3: 10
Suppose that the distribution of monthly revenues of a new startup business is not symmetric.
According to Chebyshev's Theorem, at least approximately what percentage of the revenues are within k=3.3 standard deviations of the mean?
Answers
According to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
What is Chebyshev's Theorem?
The minimum percentage of observations that are within a given range of standard deviations from the mean is calculated using Chebyshev's Theorem. Several other probability distributions can be applied to this theorem. Chebyshev's Inequality is another name for Chebyshev's Theorem. For a large class of probability distributions, Chebyshev's inequality ensures that no more than a specific percentage of values can deviate significantly from the mean.
According to Chebyshev's Theorem, at least 1 - 1/k² of the revenues lie within k standard deviations of the mean.
So when k = 3.3
1 - 1/k² = 1 - 1/3.3² = 1 - 0.0918 = 0.9082 = 90.82% ≈ 91%
Therefore according to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
To learn more about Chebyshev's Theorem, follow the link.
https://brainly.com/question/5179184
#SPJ1
A painting is 36 in. wide. Mark wants the
painting to be centered on a wall that is
144 in. wide. How much wall space will
be left on each side of the painting
Answers
144-36=108 108/2= 54
10 - 3 (z - 2) = 5z + 7
Answers
Answer:
= 9/8
That's the answer
Which equation represents a line that passes through (4, 5) and has a slope of ?
Oy- = {(x-4)
Oy- s = (x-4)
O y = 4(x -
O y-4 = }(x - 1)
=
Answers
Answer:
y- s = (x-4)
Step-by-step explanation:
Because if you sub in x = 4, y =5
you get 5 -5 = 4-4
0 = 0
Which statements are true? Select each correct answer. Responses 15m3−6m=3m(5m2−6m) 15 m cubed minus 6 m equals 3 m left parenthesis 5 m squared minus 6 m right parenthesis 40m6−4=4(10m6−1) 40 m begn power 6 end power minus 4 equals 4 left parenthesis 10 begin power 6 end power minus 1 right parenthesis 32m4+12m3=4m3(8m+3) 32 m begin power 4 end power plus 12 m cubed equals 4 m cubed left parenthesis 8 m plus 3 right parenthesis 6m2+18m=6m2(1+3m)
Answers
The true statement are:
A. 15m3-6m=3m(5m2-6m),
B. 40m6-4=4(10m6-1),
C. 6m2+18m=6m2(1+3m),
What are the true statement?15m3-6m=3m(5m2-6m) - This is true. Factoring out 3m from the terms on the left side gives 3m(5m2 - 2), which matches the right side.40m6-4=4(10m6-1) - This is true. Distributing 4 on the right side gives 4(10m6) - 4, which simplifies to the left side.6m2+18m=6m2(1+3m) - This is true. Factoring out 6m2 from the terms on the left side gives 6m2(1 + 3m), which matches the right side.32m4+12m3(8m+3) - This is not an equation or inequality, so it cannot be true or false.Therefore the correct option is A, B, C.
Learn more about parenthesis here:https://brainly.com/question/172904
#SPJ1
The correct question is:
Which statements are true
15m3-6m=3m(5m2-6m),
40m6-4=4(10m6-1),
6m2+18m=6m2(1+3m),
32m4+12m3(8m+3)
PLEASE HELP AS SOON AS POSSIBLE

Answers
Answer:
B
Step-by-step explanation:
Yes, because for each input there is exactly one output. You can have two of the same x values but you cannot have 2 of the same y values. if you have two of the same y values, it is not a function as it doesn't pass the vertical line test.
Which of the following best describes a circle?
A. The set of all points in a plane at a given distance from a given
point
O B. The set of all points in a plane that are equidistant from two points
C. The set of all points in a plane that are equidistant from a given
point and a given line
D. The set of all points smaller than or equal to a given distance from
a given point
Answers
if i run 160 meters 20 times in 2 hours how fast am i going
Answers
Answer:
1700 meters / hour
Step-by-step explanation:
160x20 = 3200
3200/ 2 = 1700
What is the greatest common factor of 72 and 90?
6
9
18
36
Answers
Answer:
It is 18.............
Answer:
______18________
Step-by-step explanation:
Find GCF.
Brainliest Plz
A bank loaned out 20,500, part of it at the rate of 9% annual interest, and the rest at 11% annual interest the total interest earned for both loans was 2,225.00 how much was loaned at each rate
Answers
The money loaned at 9% annual interest was 1500 and the money loaned at 11% annual interest was 19000.
Let the amount of money loaned at 9% be x
the amount of money loaned at 11% be y
According to the question,
Total money loaned = 20,500
Thus the equation formed is,
x + y = 20,500 ------ (i)
Simple interest is calculated by
I = P * r * t
where I is the simple interest
r is the rate of interest
t is the time
Thus, the interest on x = 0.09x
the interest on y = 0.11y
Total interest gained = 2,225
Thus the equation formed is,
0.09x + 0.11y = 2225 -------(ii)
Multiply (i) by 0.09
0.09x + 0.09y = 1845
Subtract the above from (ii)
0.02y = 380
y = 19000
x = 1500
Learn more about Equation:
https://brainly.com/question/28871326
#SPJ1
One side of a rectangle is 6 meters shorter than four times another side. Find the length of the longer side if we also know that the perimeter of the rectangle is 58 meters
Answers
Answer:
22 meters
Step-by-step explanation:
Let x = width of the rectangle
Let y = length of the rectangle
Equation 1
If the length of the rectangle is 6 meters shorter than four times the width then:
⇒ y = 4x - 6
Equation 2
Perimeter of a rectangle = 2(width + length)
If the perimeter is 58 inches, then:
⇒ 58 = 2(x + y)
Solve by substitution
Substitute Equation 1 into Equation 2 and solve for x:
⇒ 58 = 2(x + 4x - 6)
⇒ 58 = 2(5x - 6)
⇒ 58 = 2 · 5x - 2 · 6
⇒ 58 = 10x - 12
⇒ 58 + 12 = 10x -12 + 12
⇒ 10x = 70
⇒ 10x ÷ 10 = 70 ÷ 10
⇒ x = 7
Substitute found value of x into Equation 1 and solve for y:
⇒ y = 4(7) - 6
⇒ y = 28 - 6
⇒ y = 22
Conclusion
The dimensions of the rectangle are:
width = 7 meterslength = 22 metersTherefore, the length of the longer side is 22 meters
The length of the longer side is 22 meters.
Let, one side of the rectangle is x meters.
According to the problem, the other side is 6 meters shorter than four times this side, which means the length of the second side is (4x - 6) meters.
The perimeter of a rectangle is given by the formula:
Perimeter = 2 * (length + width)
In this case, the perimeter is 58 meters:
58 = 2 * (x + 4x - 6)
Now, let's solve for x:
58 = 2 * (5x - 6)
58 = 10x - 12
Add 12 to both sides:
58 + 12 = 10x
70 = 10x
Now, divide both sides by 10 to isolate x:
x = 70 / 10
x = 7
So, one side of the rectangle is 7 meters.
Now, we can find the length of the longer side:
Length of the longer side = 4x - 6
Length of the longer side = 4 * 7 - 6
Length of the longer side = 28 - 6
Length of the longer side = 22 meters
Therefore, the length of the longer side is 22 meters.
Learn more about perimeter here:
brainly.com/question/397857
#SPJ3
12. Sasha surveys students from her homeroom about the number of
siblings each student has. The results are 1, 0, 2, 2, 3, 0, 1, 1, 4,
and 5. What is the mode(s) of the data? (CC.6.SP.5c)
C 1
(D) 1 and 2
in
(A) 1.5
B 0 and 2
Answers
The calculated value of the mode(s) of the data is (a) 1
How to determine the mode(s) of the data?From the question, we have the following parameters that can be used in our computation:
1, 0, 2, 2, 3, 0, 1, 1, 4, and 5
By definition, the mode of a data is the data that has the highest frequency
Using the above as a guide, we have the following:
The data element 1 has the highest frequency of 3
Other data elements have lesser frequencies
Hence, the mode(s) of the data is (a) 1
Read more about mode at
https://brainly.com/question/14532771
#SPJ1
Need help on this!!! Pls help!!!

Answers
a) The mean of the data-set is of 2.
b) The range of the data-set is of 4 units, which is of around 4.3 MADs.
How to obtain the mean of a data-set?The mean of a data-set is obtained as the sum of all observations in the data-set divided by the number of observations in the data-set, which is also called the cardinality of the data-set.
The dot plot shows how often each observation appears in the data-set, hence the mean of the data-set is obtained as follows:
Mean = (1 x 0 + 5 x 1 + 3 x 2 + 5 x 3 + 1 x 4)/(1 + 5 + 3 + 5 + 1)
Mean = 2.
The range is the difference between the largest observation and the smallest, hence:
4 - 0 = 4.
4/0.93 = 4.3 MADs.
More can be learned about the mean of a data-set at brainly.com/question/1156334
#SPJ1
Find the time t, in years, for the principal P= $720 to reach the future value F = $735 under r = 1.74% interest compounded quarterly. Round your final answer to two decimal places.
Answers
Answer:
1.19 yearsStep-by-step explanation:
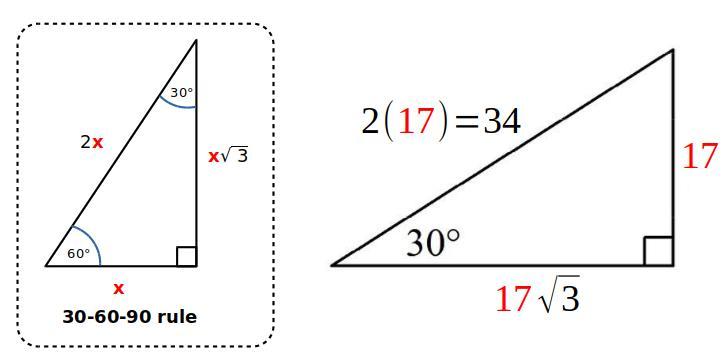
GivenP = $720F = $735r = 1.74% Compound n = 4tTime = t = ?Solution735= 720*(1 + 0.0174/4)^n1.00435^n = 735/7201.00435^n = 1.02083333333 log 1.00435^n = log 1.02083333333 n= log 1.02083333333 / log 1.00435n = 4.75t = 4.75/4t = 1.1875 = 1.19 rounded to 2 decimal placesLabel the triangle sides, assuming the angle of interest is the 30-degree angle:
solve for
The side with x is the
blank side.
The side with y is the
NO SPAM I WILL REPORT YOU
blank side.
The side with 17 is the blank side

Answers
Check the picture below.
On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 3, negative 3) and (3, 1). Everything below and to the right of the line is shaded.
Which linear inequality is represented by the graph?
y > Two-thirdsx – 2
y < Two-thirdsx + 2
y > Two-thirdsx + 1
y < Two-thirdsx – 1
Answers
Answer:
y > Two-thirds x + 1 /c
Simplify using the order of operations. 2+6*8=
Answers
Answer:
The answer is 50.
Step-by-step explanation:
Use MDAS
Multiplication, Division, Addition and Subtraction
2 + 6 * 8 =
Multiply first then add
2 + 6*8 = ?
= 2 + 48
= 50
Q1. Butternut is a ski resort in Massachusetts. One of their triple chair lifts unloads 576 skiers per hour at the top of the slope. (A triple chair lift can carry three passengers per chair.) If 108 skiers are riding on the lift at any one time, how long does the ride from the bottom to the top take
Answers
Answer:
11.25minutes
Step-by-step explanation:
From the question we are told that lifts unloads 576 skiers per hour at the top of the slope, this is expressed as;
576skiers = 1hr
To determine the time it will take 108skier, we can write
108skier = x
Divide both expressions
576/108 = 1/x
576x =108
x = 108/576
x = 0.1875hr
Convert to minute
x = 0.1875×60
x = 11.25minutes
Hence it took the ride 11.25minutes
A vector is described. Express the vector in terms of i and j. If exact values are not possible, round components to the nearest tenth.A plane with an airspeed of 440 miles per hour is flying in the direction N35°W.Question content area bottomPart 1The vector in terms of i and j is enter your response here(Type your answer in terms of i and j. Use integers or decimals for any numbers in the expression. Round the final answer to the nearest tenth as needed. Round all intermediate values to the nearest thousandth as needed.)

Answers
see the figure below to better understand the problem
Find out Rx
Rx=R*cos35
Rx=440*cos35=360.427 mph
Ry=440*sin35=252.373 mph
V=360.4i+252.4j

What else would need to be congruent to show that AABC= AXYZ by ASA?
A
B
A.
B. AC=XZ
C. BC=YZ
D. ZCE Z
C
X
Y
N
Given:
AC = XZ
ZAEX

Answers
Answer:
D
Step-by-step explanation:
ASA = 2 non included angles + 1 included side
by knowing angle c is congruent to angle z we can prove the triangles are congruent by ASA postulate.
The correct statements would need to be congruent to show that
Δ ABC= ΔXYZ by ASA are,
⇒ ∠ B ≅ ∠ Y
⇒ ∠ C ≅ ∠ Z
What is mean by Angle?An angle is a combination of two rays (half-lines) with a common endpoint. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle.
Given that;
AC = XZ
∠ A = ∠ X
Now, To prove the triangles are congruent by ASA , we get;
AC = XZ
∠ A = ∠ X
⇒ ∠ Z = ∠ C
or, ∠ B = ∠ Y
Thus, The correct statements would need to be congruent to show that
Δ ABC= ΔXYZ by ASA are,
⇒ ∠ B ≅ ∠ Y
⇒ ∠ C ≅ ∠ Z
Learn more about the angle visit:;
https://brainly.com/question/25716982
#SPJ5
What is the equation in slope-intercept form of the line that passes through the point (6, 1) and is parallel to the line represented by
y = -3x + 2?
Enter your answer by filling in the boxes.
Answers
Mathematical 8. PRACTICE Model Math Christy purchased 6.75 pounds of licorice. How much licorice does she need to put in each bag if she divides the total amount into 10 equal-sized bags?
Answers
Answer:i think it is yes! this )--89+98
Step-by-step explanation:
Find the differential of the function w=x^(4)sin(y^(4)z^3)

Answers
Step-by-step explanation:
\(w = x^4\sin(y^4z^3)\)
The differential \(dw\) is
\(dw = 4x^3\sin(y^4z^3)dx \)
\(\:\:\:\:\:\:\:\:\:\:\:+ x^4\cos(y^4z^3)(4y^3z^3)dy \)
\(\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+ x^4\cos(y^4z^3)(3y^4z^2)dz\)
84.4% of what number is 19.412?
Answers
Answer: 22.4402
Step-by-step explanation:
Answer:
84.4% of 23 is 19.412.
Step-by-step explanation:
Let the unknown number be x.
Now, 84.4% of x = 19.412.
∴ (84.4 ÷ 100) × x = 19.412.
By simplifying the equation,
x = (19.412 × 100) ÷ 84.4
x = 1941.2 ÷ 84.4
∴ x = 23
Thus, 84.4% of 23 is 19.412.
To learn more about Percentages,
refer to the following question!
https://brainly.com/question/3079428