thank you for the people who helped me on the other can you also help me on this one?????

Answer:

answer is \(\frac{23}{63}\)

Step-by-step explanation:

the equation is

\(\frac{5}{63}-(-\frac{6}{21} )\)

=> \(\frac{5}{63}+\frac{6}{21}\)

=> \(\frac{5}{63}+\frac{2}{7}\) ;(divide numerator and denominator of \(\frac{6}{21}\) by 3)

=> \(\frac{5+2*9}{63}\)

=> \(\frac{23}{63}\)

hope you have understood this

pls mark it as the brainliest

Answer:

4 boys

Step-by-step explanation:

\(\frac{1}{3} :\frac{y}{12}\)

3 × y = 1 × 12

3y = 12

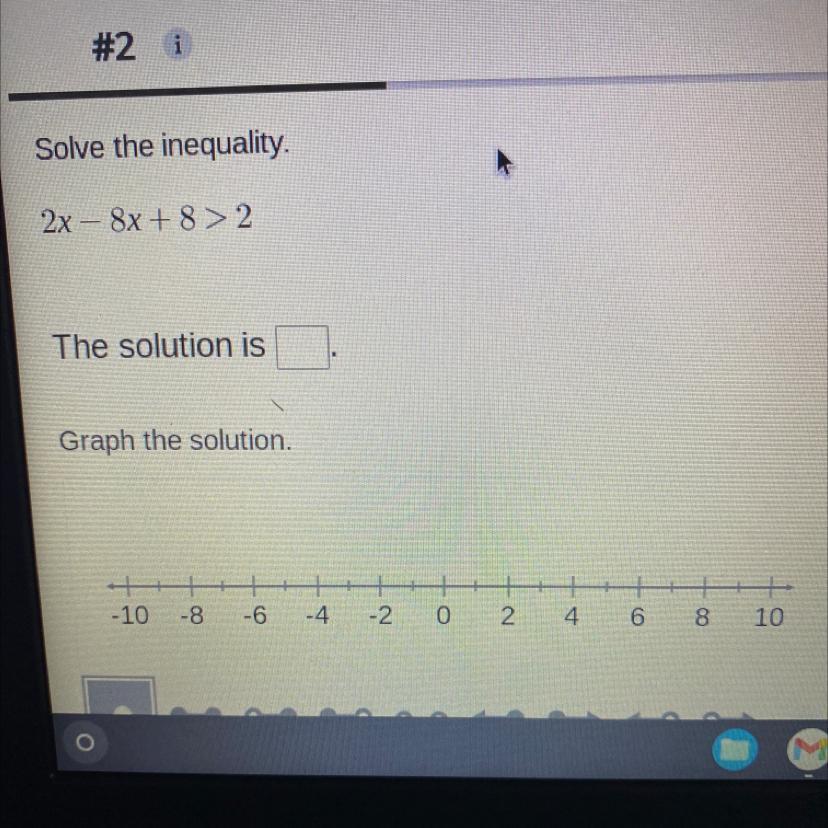
3y ÷ 3 = 12 ÷ 3

y = 4

Answer:

The current temperature = 34.2°C

Step-by-step explanation:

Initial temperature = 46.8°C

After 20 minutes temperature reduced by 12.6°C

Therefore, the current temperature is = 46.8°C - 12.6°C = 34.2°C

Answer: x=-6

Step-by-step explanation:

9(x+3)=4x-3

9x+27=4x-3 ⇔ distributive property (take off parentheses)

5x+27=-3 ⇔ subtraction property of equality (subtract 4x on both sides)

      5x=-30 ⇔ subtraction property of equality (subtract 27 on both sides)

        x=-6

Hope this helps!! :)

Please let me know if you have any question

Answer:

simplify both sides and get 9x+27=4x+−3 then subtract 4x and get  5x+27=−3 and subtract -27 and divide answer by 5 to get x=-6

Answer:

= − 4 3

Step-by-step explanation:

Answer:

x+62=19

x=19-62

x=-43

I hope this help

Answer:

Step-by-step explanation:

Answer:

249.6

Step-by-step explanation:

width x height x 1/2 = area fo a triangle

12(2) x 10.4(2) x 1/2 = 249.6

I assumed this means all of the surface area. Hope this helps. Sorry if I'm wrong.

Answer:

x = 92

Step-by-step explanation:

Equation: x + 12 = 104

104 - 12 = 92

Answer:

x+12=104

x=92

Step-by-step explanation:

Subtract 12 from 104 to get your answer

The value of expression is,

⇒ x ÷ 12

We have to given that;

The algebraic expression is,

⇒ x divided by 12

Hence, We can formulate;

The value of correct expression is,

⇒ x ÷ 12

⇒ x / 12

Thus, The value of expression is,

⇒ x ÷ 12

Learn more about the mathematical expression visit:

brainly.com/question/1859113

#SPJ1

To determine if there is a difference in the average percentage of season games of their favorite sport a fan attends based on if their favorite sport is baseball or basketball, we would need to conduct a study and collect data on both baseball and basketball fans.

We would then calculate the average percentage of season games attended by each group and compare the results.

If there is a statistically significant difference between the two groups, we can conclude that there is a difference in the average percentage of season games attended based on favorite sport.

Learn more about percentage:

https://brainly.com/question/24304697

#SPJ11

Answer: How to calculate commission. This is a very basic calculation revolving around percents. Just take sale price, multiply it by the commission ...

Step-by-step explanation:

The factorized expressions is 3(x-4)(x-5).

We are given that;

The expression 3x² - 27x+60​

Now,

1.1.1 After simplification

-3(2x - 4y)² = -12(x-y)²

1.1.2 x+2/3*5x+1

= (3x+5)/(3x+3)

1.2.1 ny + 4z + 4y + nz

= (n+4)(y+z)

1.2.2 3x² - 27x+60

= 3(x-4)(x-5)

Therefore, by the expression the answer will be 3(x-4)(x-5).

To know more about an expression follow;

brainly.com/question/19876186

#SPJ1

The vector-valued function at each given value of t  is :

a) i

b)  1/√2i+9/√2j

c)−cos(θ)i+9sin(θ)j

d)  −2sin(π/6+△t/2)sin(△t/2)i+18cos(π/6+△t/2)sin(△t/2)j

The given problem is related to trigonometric Ratios of Angle, where there are six trigonometric ratios sine, cosine, tangent, cotangent, cosecant, and secant. Since it is given that a  vector valued function:

r(t)= cos(t)i + 9 sin(t)j

r(t)=cos(t)i+9sin(t)j

so ,  r(0)=  cos(0)i+9sin(0)j = i ( sine cos0 =1 and sin0 =0)

r(π/4) =  cos(0)i+4sin(0)j = cos(π/4)i+9sin(π/4)j

           = 1/√2i+9/√2j

r(θ−π)= cos(θ−π)i+9sin(θ−π)j= −cos(θ)i+9sin(θ)j

(π/6+△t)−r(π/6)= cos(π/6+△t)i+9sin(π/6+△t)j−cos(π/6)i−9sin(π/6)j

=  cos(π/6+△t)i−cos(π/6)i+9sin(π/6+△t)j−9sin(π/6)j

= −2sin(π/6+△t/2)sin(△t/2)i+18cos(π/6+△t/2)sin(△t/2)j

to know more about vectors refer to the link https://brainly.com/question/19754999?referrer=searchResults.

#SPJ4

Evaluate (If possible) the vector-valued function at each given value of t. (If an answer does not exist, enter DNE.)

r(t)=cos(t)i+9sin(t)jr(t)

a)r(0)=?

b)r(π/4)=?

c)r(θ−π)=?

d)r(π/6+△t)−r(π/6)=?

Answer:

The final cost after the discount and tax is $179.76

Step-by-step explanation:

Since the discount is 30%, she only pays 70% of the price of the ticket.

Discounted price before tax:

70% of $240 = 0.7 × $240 = $168

Now think of the price $168 as a new price.

The price is $168 which is 100% of the price. Tax is 7% of the price, so you must pay 107% of the price.

107% of $168 = 1.07 × $168 = $179.76

Answer: The final cost after the discount and tax is $179.76

For 10 animals do Jose and Nancy charge the same amount.

For, the given question;

Let there be 'x' number of animals.

Jose charges $15 plus $2 per animal.

15 + 2x

And, Nancy charges $5 plus $3 per animal.

5 + 3x

Then,

For the same amount, equate both equations.

15 + 2x = 5 + 3x

On solving;

x = 10

Thus, for 10 animals, their total charge will be equal.

To know more about the linear equation, here

https://brainly.com/question/2030026

#SPJ9

According to the results shown in the chart, if the cube is rolled 50 times, it should fall on 1 about 7 times.

A number that connects a component to a whole is a proportion. For instance, there are 100 students in the classroom with 20 males and 80 women. The percentage of men is 20/100, or 20%. 80 out of 100, or 80%, are women.

We can find the expected number of times the cube lands on 1 if it is rolled 50 times by calculating the proportion of times 1 was rolled in the 200 trials and then scaling it to 50 rolls:

Expected number of times 1 is rolled = (Proportion of times 1 was rolled) x (Number of rolls)

Proportion of times 1 was rolled = (Number of times 1 was rolled) / (Total number of rolls) = 28/200 = 0.14

Expected number of times 1 is rolled = (0.14) x (50) = 7

Therefore, the cube is expected to land on 1 about 7 times if it is rolled 50 times based on the outcomes observed in the table.

To know more about Proportion visit:

https://brainly.com/question/1496357

#SPJ1

If a gardener can care for the greens property in 5 hours and if his helper assists him, they will be done in 4 hours, then the number of hours it takes for the helper to do it alone is equal to 20.

The number of hours it takes for the helper to do it alone can be found as follows;

Time taken by both the gardener and the helper to complete the job=4

Work done by both the gardener and the helper in one hour = 1/4

Similarly,

Time taken by the gardener to complete the job = 5

Work done by the gardener in one hour = 1/5

The number of hours it takes for the helper alone can be calculated by subtraction. Subtracting the fraction done by the gardener in 1 hour from the fraction done by both the gardener and the helper in 1 hour;

1/4 - 1/5

As the common denominator is 20, we multiply 1/4 by 5 and 1/5 by 4.

5/20 - 4/20 = 1/20

The number of hours it takes for the helper to do it alone can be found by finding the reciprocal of 1/20 which is equal to 20/1

20/1 = 20

Hence, the helper takes 20 hours to do it alone.

To learn more about subtraction, click here:

https://brainly.com/question/13378503

#SPJ4

A. The proof is correct. By starting with the assumption that n is an arbitrary integer, it sets up universal generalization. Then it makes a case distinction, so that no matter whether n is even or odd, k comes out to be odd, and between n and n+3. By universal generalization, that proves that such k exists for all integers n. is the correct option.

Each of the following proofs is an attempt to prove the statement "For every integer n, there is an odd number k such that n < k < n + 3." Only one of the proofs is correct. The correct analysis of each proof's merits is as follows:A. The proof is correct. By starting with the assumption that n is an arbitrary integer, it sets up universal generalization. Then it makes a case distinction, so that no matter whether n is even or odd, k comes out to be odd, and between n and n+3. By universal generalization, that proves that such k exists for all integers n.B.

This proof shows that for every odd k, an integer n with n < k < n+3 exists, which is a different statement than what was supposed to be proved, and not logically equivalent. C. The proof starts with the proper assumption but constructs the wrong k. While the k is between n and n+3, it may not be odd. The k chosen is even when n is even.D. The proof starts with the proper assumption, but then constructs the wrong k. 2n+1 while odd, is generally not between n and n+3.Long answer: For every integer n, there is an odd number k such that n < k < n + 3 is the statement that is given in the question.

Now, the proofs are as follows:

Proof 1: Let the integer n be given. If n is even, let k be n + 1. If n is odd, let k be n + 2. Either way, k is odd and n < k < n + 3. That proves that for any integer n, an odd k such that n < k < n + 3 exists. This proof is correct. By starting with the assumption that n is an arbitrary integer, it sets up universal generalization. Then it makes a case distinction, so that no matter whether n is even or odd, k comes out to be odd, and between n and n+3. By universal generalization, that proves that such k exists for all integers n.

Proof 2: Given the integer n, pick k - n + 2. Then n < k < k + 3. Thus, for every integer n, an odd k with n < k < n + 3 exists. This proof shows that for every odd k, an integer n with n < k < n + 3 exists, which is a different statement than what was supposed to be proved, and not logically equivalent.

Proof 3: Let n be given. Then k = 2n + 1 is odd by definition, and greater than n. Since also k < n + 3, we have shown the existence of an odd k between n and n + 3 for all n. This proof starts with the proper assumption but constructs the wrong k. 2n+1 while odd, is generally not between n and n+3.

Proof 4: Let the odd integer k be given. Pick n = k - 1. Then n < k < n + 3. We have shown that for every integer n, an odd integer k with n < k < n + 3 exists. This proof starts with the proper assumption, but then constructs the wrong k. It does not specify that k is between n and n+3.

To know more about integer visit:

https://brainly.com/question/32680508

#SPJ11

False. The average value of a constant function does not change over different intervals, so the average value of f(x) at [1,10) would still be c.

A constant function has the same value for all x-values in its domain. If the average value of f(x) at [1,5] is c, it means that the function has the value c for all x-values in that interval.

Now, when considering the interval [1,10), we can observe that it includes the interval [1,5]. Since f(x) is a constant function, its value remains c throughout the interval [1,10). Therefore, the average value of f(x) at [1,10) would still be c.

In other words, the average value of a function over an interval is determined by the values of the function within that interval, not the length or range of the interval. Since f(x) is a constant function, it has the same value for all x-values, regardless of the interval.

Thus, the average value of f(x) remains unchanged, and it will still be c for the interval [1,10).

Learn more about average value of a constant function:

https://brainly.com/question/27490113

#SPJ11

Answer:

Step-by-step explanation:

Let sharma age be S and Ankit age be A

S = 3a

(s-10) = 5(a-10)

substitute 1 in 2

3a-10 = 5a -50

40 = 2a

a = 20

s = 3 * 20 = 60

The upper bound confidence interval for the population mean weekly wages at a 95% level of confidence is ($411.89, $443.51).

To calculate the confidence interval, we can use the t-distribution since the population standard deviation is unknown and we have a small sample size (n = 21).

First, we need to calculate the standard error (SE) which is the sample standard deviation (s) divided by the square root of the sample size (√n). In this case, SE = $104.25 / √21 ≈ $22.72.

Next, we need to determine the critical value of the t-distribution for a 95% confidence level with (n-1) degrees of freedom. With 20 degrees of freedom, the critical value is approximately 2.086.

The margin of error (ME) is then calculated by multiplying the standard error by the critical value: ME = 2.086 * $22.72 ≈ $47.36.

Finally, the confidence interval is constructed by subtracting the margin of error from the sample mean (7) and adding it to the sample mean: ($427.7 - $47.36, $427.7 + $47.36) = ($411.89, $443.51).

Interpretation:

We are 95% confident that the true average weekly wages of farm workers in the rural county falls within the range of $411.89 and $443.51. This means that if we were to take multiple samples and construct confidence intervals, approximately 95% of them would contain the true population mean.

Learn more about population:

brainly.com/question/15889243

#SPJ11

Answer:

I am writing a Python program:

def most_common_letter (string):  #function that takes a string as argument and returns the most commonly occurring letter in string

   string = string.lower()  # converts the string into lower case

   inp_string="".join(string.split())  #splits the string in to a list and joins the elements of the list

   maximum = 0  #sets the value of maximum to 0

   letter = ""  #stores the most commonly occurring letter

   length = len(inp_string)  #returns the length of the input string

   counter = 0  #counts the occurrences of the letter in the string

   for i in range(0, length):  # iterates through the length of string        

       j = 0  #initializes j to 0

       char = inp_string[i]  #  holds letter of input string at index position i

       while length > 0:  # iterates until the length of string exceeds 0

           if (char == inp_string[j]):  # if letter in char is equal to letter at index j of the string

               counter += 1  #adds 1 to the count

           j += 1  #increments j by 1

           length -= 1    #decrements value of length by 1

           if (maximum <= counter):  #if maximum value is less than counter

               maximum = counter  #sets the maximum number of occurrences of a letter to maximum

               letter = char #sets the most occuring letter in string to letter

   return letter  #returns the most commonly occurring letter in the input string

#in order to check if the function works properly use following statement

print(most_common_letter("This is a test of the function I have written")) #calls most_common_letter method by passing a string to it

Step-by-step explanation:

The program works as follows:

I will explain this with the help of an example. Suppose the string is:

string = "hello worLd"

first this string is converted to lowercase using lower() method. So the string becomes:

string = "hello world"

Next the string is split into a list using split() method. The string becomes:

['hello', 'world']

Then using join() this string is joined together on the basis of "" empty space

So the string becomes

helloworld

This string is assigned to the inp_string variable. Hence

inp_string = "helloworld"

The value of maximum is initialized to 0 and variable letter is also declared

which holds the most commonly occurring letter in the inp_string

len function is used to get the length of the inp_string

counter is initializes to 0. This counts the number of times the letter occurs in a string

The for loop iterates through the inp_string

Inside the loop the statement char = inp_string[i] sets the letter at the i-th index of inp_string to char.

i is initialized to 0 so inp_string[i] is inp_string[0] which is the first element of the string i.e. "h".

The program control then moves to the while loop. As length>0 so the program moves to the body of while loop which has an if statement:            if (char == inp_string[j]):      

This checks if the letter stored in char is equal to the letter at j-th index of the string. Now as j is initialized to 0. So

if (char == inp_string[0]):   this evaluates to true and value of counter is incremented to 1. Next value of j also incremented to 1 and length of string is decremented to 1 Hence

counter = 1

j = 1

length = 9

Next if (maximum <= counter): condition checks if value of maximum is less than or equal to counter. It is true because maximum=0 and counter =1

So    maximum = counter  assigns counter value to maximum and letter = char assigns char to letter which was initially empty.

  maximum = 1

  letter = 'h'

At occurrence each iteration each letter in a string is counted and the letter that occurs the most in the string is returned by the function. For the above example hello world, letter l appears 3 times in the string and it is the most commonly occurring letter in the input string. So letter "l" is returned by this function. Hence the output of this program is l.

Answer:

Es la b

Step-by-step explanation:

Answer: are there any other pictures or other ways to word it?

Answer:

answer:250 pieces

1 metre=100cm so

10metres =100*10 =1000cm

each piece is 4 CM long, so.,

no. of pieces=1000/4

by dividing by 2....

=500/4

again by dividing by2...

=250/1=250 pieces

so 250 pieces of ribbon can be cuttted from 10 metre long ribbon.

Answer:

D

Step-by-step explanation:

14.34 x 21 - 2.40 x 7 = 284.55

Therefore, the amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity is $7,366.99. Option (d) is correct.

An account paying 4.6% interest compounded quarterly has a balance of $506,732.32.

The amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity is $7,366.99 (option D). Explanation: An ordinary annuity refers to a series of fixed cash payments made at the end of each period.

A typical example of an ordinary annuity is a quarterly payment of rent, such as apartment rent or lease payment, a car payment, or a student loan payment. It is important to understand that the cash flows from an ordinary annuity are identical and equal at the end of each period. If we observe the given problem,

we can find the present value of the investment and then the amount that can be withdrawn quarterly from the account for 20 years, assuming an ordinary annuity.

The formula for calculating ordinary annuity payments is: A = R * ((1 - (1 + i)^(-n)) / i) where A is the periodic payment amount, R is the payment amount per period i is the interest rate per period n is the total number of periods For this question, i = 4.6% / 4 = 1.15% or 0.0115, n = 20 * 4 = 80 periods and A = unknown.

Substituting the values in the formula: A = R * ((1 - (1 + i)^(-n)) / i)where R = $506,732.32A = $506,732.32 * ((1 - (1 + 0.0115)^(-80)) / 0.0115)A = $506,732.32 * ((1 - (1.0115)^(-80)) / 0.0115)A = $7,366.99

Therefore, the amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity is $7,366.99. Option (d) is correct.

To know more about periods visit:

https://brainly.com/question/23532583

#SPJ11

Answer:

y = -4/5 x - 5

Step-by-step explanation: