Warren bought a shirt on sale for $25. the original price of the shirt was 3 times that amount. warren also bought a pair of shoes on sale for $29. the original price of the shoes was 4 times that amount. together, how much money did the shirt and shoes cost before they went on sale?
Answers
Answer:
$191
Step-by-step explanation:
The shirt is $25 but the original price before it went on sale is= 3 times $25= $75
The shoes is $29 but the original price before it went on sale is= 4 times $29= $116
All together before it went on sale is $116+$75= $191.
Related Questions
3. Juanita has been offered a job that pays $497.35 for a 35-hour work week. A second
company offers her a job at $16.75/h, but will only guarantee 30 hours per
week.
Which job would you advise Juanita to take?
Answers
Answer:
The second job because, it pays more and it has less hours.
Step-by-step explanation:
Marco has two bags of candy. One bag contains three red lollipops and
2 green lollipops. The other bag contains four purple lollipops and five blue
lollipops. One piece of candy is drawn from each bag. What is the probability
of choosing a green lollipop and a purple lollipop?
Answers
The value of the probability of choosing a green lollipop and a purple lollipop is, 8 / 45
We have to given that;
One bag contains 3 red lollipops and 2 green lollipops.
And, The other bag contains four purple lollipops and five blue lollipops.
Hence, The probability of choosing a green lollipop is,
P₁ = 2 / 5
And, The probability of choosing a purple lollipop is,
P₂ = 4 / 9
Thus, The value of the probability of choosing a green lollipop and a purple lollipop is,
P = P₁ × P₂
P = 2/5 × 4/9
P = 8/45
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
You work in Social Media as a consultant. You are working on a new report to examine trends in Social Media usage and age. You conducted a survey of 1072 people randomly selected in the United States (you limited minimum age to 12). The file "Usagef.xlsx" has results of the survey. For each Social Media platform you have a 0/1 variable indicating whether or not the person said they used the platform in the last 6 months. For each of those variables, 1 means the person did use the platform in the last 6 months and 0 means they did not. You also have the age of each respondent calculated based on birth date (so 43.56 means the individual is 43.56 years old). There are two additional variables:
Young adult: 1=respondent is under 35; 0=respondent is 35 or over.
Platforms Used: The total number of Social Media platforms used in the last 6 months.
Please use this information and the data in the excel spreadsheet "Usagef.xlsx" to answer the following questions:
Assuming the sample is a random sample of the U.S. population, what is the upper bound of the 95% confidence interval for the average age in the U.S?
Answers
The upper bound of the 95% confidence interval for the average age in the U.S. is 48.29 years.
To determine the upper bound of the 95% confidence interval for the average age in the U.S., we can use the sample data from the survey. The sample size is 1072 people, randomly selected from the U.S. population, with a minimum age of 12. By calculating the average age of the respondents, we can estimate the average age of the entire U.S. population.
Using the given information that the average age of the respondents is 43.56 years, and assuming that the sample is representative of the population, we can calculate the standard error. The standard error measures the variability of the sample mean and indicates how much the sample mean might deviate from the population mean.
Using statistical methods, we can calculate the standard error and construct a confidence interval around the sample mean. The upper bound of the 95% confidence interval represents the highest plausible value for the population average age based on the sample data.
Therefore, based on the provided information and calculations, the upper bound of the 95% confidence interval for the average age in the U.S. is 48.29 years.
Learn more about Confidence intervals
brainly.com/question/32546207
#SPJ11
Can somebody help me please? thank you.

Answers
hope this helps :)
Determine if the triangles are congruent by HL, SAS, SSS, AAS, or
ASA
Somebody help please!!!

Answers
Please help answer
A ans C please
on the image.

Answers
7x-1 is less than or equal to 62 answer
Answers
The value of the variable is 9
How to determine the valueIt is important to note that inequalities are described as non- equal comparison of numbers or expressions.
The signs of inequalities represents;
< represents less than> represents greater thanFrom the information given, we have that;
7x - 1 is less than or equal to 62
This is represented as;
7x - 1≤ 62
collect the like terms, we have;
7x ≤ 62 + 1
Add the values
7x ≤ 63
Divide both sides by the coefficient, we get;
x ≤ 63/7
x ≤ 9
Learn more about inequalities at: https://brainly.com/question/25275758
#SPJ1
At which value in the domain does f(x)=0? On a coordinate plane, a function goes through the x-axis at (negative 2.5, 0), (negative 0.75, 0), (0, negative 3), and (1, 0).
Answers
Answer:
The values in the domain where f(x) = 0 are x = -2.5, x = - 0.75 and x = 1.
Step-by-step explanation:
Since we are given the points (-2.5,0), (-0.75, 0), (0, -3) and (1,0) where the coordinates are in ordered pairs of (x, y) where y = f(x).
To find the values in the domain where f(x) = 0, we look at the ordered pairs given.
We look for the pair in which f(x) = 0.
So f(x) = 0 in (-2.5, 0)
f(x) = 0 in (-0.75, 0)
and f(x) = 0 in (1, 0)
The corresponding values of x in which f(x) = 0 are x = -2.5, x = - 0.75 and x = 1.
So, the values in the domain where f(x) = 0 are x = -2.5, x = - 0.75 and x = 1.
Answer:
C. \(x=1\)
Step-by-step explanation:
When x is 1, y is 0.
Question 3 The Schwarzschild metric is given by 2M 2M ds² -(₁-²M) di² + (1-²¹)- 1- dr² +r² (d0² + sin² 0 dó²). There are Killing vectors associated with time invariance and angular momen- tum invariance in the direction in this geometry leading to the conserved quantities e = (1-2) and l= r² sin² 0 dr From this one can derive an analog to the radial energy equation in Newtonian mechanics by orienting the coordinates so that the orbits are confined to the equatorial plane where 0 = π/2 and u = 0. One finds 2 1 dr + Veff (r) = E 2 dr (e²_ -1) where E = and Veft(r) = - + 2/²/²2 - Mp³². Further, for circular orbits one can show that M | [₁ + √/₁−12 (+1)]. r+= | 2M Finally, for circular orbits of radius R do 1/2 M dt R³ (a) Which value of r corresponds to the Schwarzschild radius of stable circular orbits: r or r? Justify your answer. [3 marks] (b) Show that for circular orbits of radius R do 1/2 M -1/2 3M (²) ¹² (1-³) dT R³ R where is the proper time. [6 marks] (c) A free particle is moving in a circular orbit around a spherical source of curvature of mass M. The Schwarzschild radius of the orbit is 8M. Use the equivalence principle to argue that the period as measured at infinity should be larger than that measured by the particle. [4 marks] (d) Find the period of the orbit as measured by an observer at infinity. Find the period of the orbit as measured by the particle. [7 marks] M
Answers
(A) Circular orbits of stable particles are possible at radii greater than three times the Schwarzschild radius for the non-rotating spherically symmetric mass.
This represents the radius of a black hole's event horizon, within which nothing can escape. The Schwarzschild radius is the event horizon radius of a black hole with mass M.
M can be calculated using the formula: r+ = 2Mwhere r+ is the radius of the event horizon.
(B) 1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ R. This is the required expression.
Tau is the proper time of the particle moving around a circular orbit. Hence, by making use of the formula given above:1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ dt.
(C) Time passes differently in different gravitational fields, and it follows that the period as measured at infinity should be larger than that measured by the particle.
The principle of equivalence can be defined as the connection between gravitational forces and the forces we observe in non-inertial frames of reference. It's basically the idea that an accelerating reference frame feels identical to a gravitational force.
(D) The period of the orbit as measured by an observer at infinity is 16π M^(1/2) and the period of the orbit as measured by the particle is 16π M^(1/2)(1 + 9/64 M²).
The period of orbit as measured by an observer at infinity can be calculated using the formula: T = 2π R³/2/√(M). Substitute the given values in the above formula: T = 2π (8M)³/2/√(M)= 16π M^(1/2).The period of the orbit as measured by the particle can be calculated using the formula: T = 2π R/√(1-3M/R).
Substitute the given values in the above formula: T = 2π (8M)/√(1-3M/(8M))= 16π M^(1/2)(1 + 9/64 M²).
To know more about Schwarzschild radius
https://brainly.com/question/29534114
#SPJ11
Jacob traveled 171 miles in 3.8 hours. He wants to know how many miles he traveled in one hour, so he set up this problem:
171 divided by 3.8
Jacob started by multiplying the divisor and the dividend by 10. This is the new problem:
1710 divided by 38
Use long division to find the quotient.
0.45
4.5
45
450
Answers
The answer is 45
------------------------------------------------------------
tsThe table below represents the concessions sold at the last three basketball games. Thegames were held on different days and times.Friday nightSaturday morningTuesday nightTotalCandy1489478320Hot Dogs10227150279Nachos Total1084297247358163325846What is the approximately probability of a person buying a hot dog and going to a Tuesdaynight game?

Answers
Given:
The total = 846.
The number of hot dogs sold at Tuesday night = 150.
Required:
We need to find the approximate probability of a person buying a hot dog and going to a Tuesday night game.
Explanation:
The total possible outcomes = 846.
\(n(S)=846\)Let A be the given event.
The favourable outcomes = The number of hot dogs sold at Tuesday night = 150.
\(n(A)=150\)The approximate probability of a person buying a hot dog and going to a Tuesday night game.
\(P=\frac{n(A)}{n(S)}\times100\)\(P=\frac{150}{846}\times100\)\(P=17.7\)\(P=18\text{ \%}\)Final answer:
\(P=18\text{ \%}\)plsss help asap first to answer gets brainest
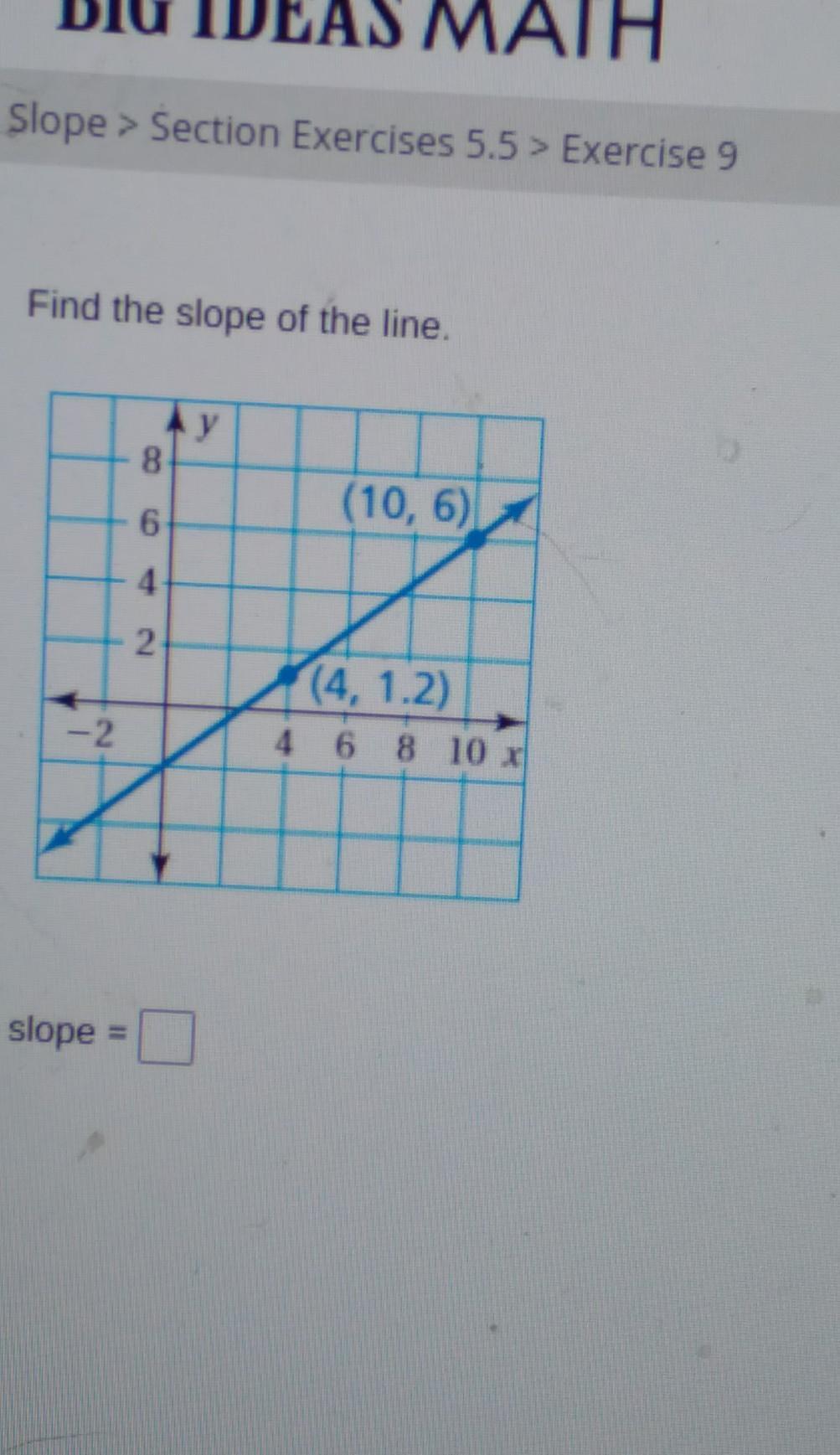
Answers
and the run is 4
Using the 100/50/20 Rule for daily fluid requirements (DFR). Calculate the following questions, do not round the patient's weight but round all final answers to a whole number. 1-10 kg = 100ml/kg/day 11-20 kg = 50ml/kg/day (+ 1000 mL/day for 1* 10kg) Over 20kg = 20mL/kg/day (1500 mL/day for 1s 20kg) 18. An infant weighs 11 pounds. What is the required amount of fluid per day in ml? I 19. A child weighs 31 lbs and 8 ozs. What is the required amount of fluid per day in ml? If no oral fluids are consumed, what is the hourly IV flow rate to maintain proper hydration?
Answers
18. An infant weighs 11 pounds which is equivalent to 4.98 kg. Using the 100/50/20 Rule, the required amount of fluid per day for an infant between 11-20 kg is 50 ml/kg/day. So, the required amount of fluid per day in ml is 4.98 kg x 50 ml/kg/day = 249 ml/day.
19. A child weighs 31lbs and 8 ozs which is equivalent to 14.21 kg. Using the 100/50/24 Rule, the required amount of fluid per day for a child over 20 kg is 20 ml/kg/day. So, the required amount of fluid per day in ml is 14.21 kg x 20 ml/kg/day = 284.2 ml/day.
If no oral fluids are consumed, the hourly IV flow rate to maintain proper hydration would be: 284.2 ml/day / 24 hours/day = 11.8 ml/hour.
Daily Fluid Requirements (DFR)The question is about fluid requirements for infants and children, and it is using the 100/50/20 Rule for Daily Fluid Requirements (DFR) to calculate the required amount of fluid per day for different weight ranges. The 100/50/20 Rule is a guideline used to determine the appropriate amount of fluid that infants and children should receive on a daily basis based on their weight. The rule states that for infants and children up to 10 kg, the recommended fluid intake is 100 ml/kg/day, for those between 11-20 kg it is 50 ml/kg/day, and for those over 20 kg it is 20 ml/kg/day.
The question also asking about the hourly IV flow rate to maintain proper hydration if no oral fluids are consumed.
This subject is part of pediatrics, more specifically in the field of fluid and electrolyte balance and management.
Learn more about Daily Fluid Requirements (DFR) here:
https://brainly.com/question/28334028
#SPJ4
find the value of m .

Answers
Step-by-step explanation:
if the 2 matrices are inverse, then their product must be the identity matrix
1 0
0 1
so,
m×3 + 2×-7 = 1
7×3 + 3×-7 = 0
m×-2 + 2×m = 0
7×-2 + 3×m = 1
that means we have to solve only
3m - 14 = 1
3m = 15
m = 5
Miriam was testing � 0 : � = 18 H 0 :μ=18H, start subscript, 0, end subscript, colon, mu, equals, 18 versus � a : � < 18 H a :μ<18H, start subscript, start text, a, end text, end subscript, colon, mu, is less than, 18 with a sample of 7 77 observations. Her test statistic was � = − 1.9 t=−1.9t, equals, minus, 1, point, 9. Assume that the conditions for inference were met.
Answers
The requreid Miriam's test does not provide significant evidence that the true population mean is less than 18.
Since the sample size is small (n = 7) and the population standard deviation is unknown, we should use a t-test for this hypothesis test.
The test statistic is calculated as follows:
t = (x - μ) / (s / √n)
Given that Miriam's test statistic is t = -1.9, we can estimate the p-value associated with this test statistic. This denotes the probability of observing a test statistic as extreme as -1.9 or more extreme, assuming the null hypothesis is true.
Using a t-distribution table with 6 degrees of freedom (n-1), we find that the p-value for a one-tailed test at the 5% significance level is approximately 0.051.
Since the p-value (0.051) is greater than the significance level (0.05), we fail to reject the null hypothesis. We do not have sufficient evidence to conclude that the population mean is less than 18 at a 5% level of significance.
Thus, Miriam's test does not provide significant evidence that the true population mean is less than 18.
Learn more about the hypothesis here:
https://brainly.com/question/29519577
#SPJ1
)) A rectangle has an area of 117.8 square kilometers and a height of 9.5 kilometers. What
is the length of the base?
kilometers
Answers
Answer:
yes you use kilometers
Step-by-step explanation:
How many solutions are there for the following equation? Why?
8(x+9)=72−5x
Answers
Answer:
1 solution , x = 0
Step-by-step explanation:
8(x + 9) = 72 - 5x ← distribute parenthesis on left side
8x + 72 = 72 - 5x ( add 5x to both sides )
13x + 72 = 72 ( subtract 72 from both sides )
13x = 0 ⇒ x = 0
x = 0 is the only solution to the equation
6.
5. The florist has 90 roses to arrange. After 5 vase
arrangements, there are 50 roses left. How
many total vase arrangements will be needed to
have only 10 roses left?
Answers
Answer:
1 vase arrangement when 10 roses are left
Step-by-step explanation:
1. so 50 divided by 5 is 10.
That means every arrangement is 10 roses.
2. it asks us to find how many vase arrangement will be needed to have only 10 roses left. We already know that we only need 1 arrangement, because we already found that out in step 1.
what is the scale factor?

Answers
Use this:
The basic formula to find the scale factor of a figure is: Scale factor = Dimensions of the new shape ÷ Dimensions of the original shape. This can also be used to calculate the dimensions of the new figure or the original figure by simply substituting the values in the same formula.
Answer:
1 2/3 is the scale factor
Step-by-step explanation:
So the scale factor either makes soemthing bigger or smaller
In this case it’s getting bigger
So we have one side already so we jsut find the value that was multiplied
so 9 * ? Is 15
You
d get 1 2/3
Verify that the inverse of A™ is (A-')?. Hint: Use the multiplication rule for tranposes, (CD)? = DCT.
Answers
The inverse of the transpose of matrix A is equal to the transpose of the inverse of matrix A.
To verify that the inverse of A transpose (A^T) is equal to the transpose of the inverse of A (A^-1), we can use the multiplication rule for transposes, which states that (CD)^T = D^T * C^T.
Let's assume that A is an invertible matrix. We want to show that (A^T)^-1 = (A^-1)^T.
First, let's take the inverse of A^T:
(A^T)^-1 * A^T = I,
where I is the identity matrix.
Now, let's take the transpose of both sides:
(A^T)^T * (A^T)^-1 = I^T.
Simplifying the equation:
A^-1 * (A^T)^T = I.
Since the transpose of a transpose is the original matrix, we have:
A^-1 * A^T = I.
Now, let's take the transpose of both sides:
(A^-1 * A^T)^T = I^T.
Using the multiplication rule for transposes, we have:
(A^T)^T * (A^-1)^T = I.
Again, since the transpose of a transpose is the original matrix, we get:
A * (A^-1)^T = I.
Now, let's take the transpose of both sides:
(A * (A^-1)^T)^T = I^T.
Using the multiplication rule for transposes, we have:
((A^-1)^T)^T * A^T = I.
Simplifying further, we get:
A^-1 * A^T = I.
Comparing this with the earlier equation, we see that they are identical. Therefore, we have verified that the inverse of A transpose (A^T) is equal to the transpose of the inverse of A (A^-1).
In conclusion, (A^T)^-1 = (A^-1)^T.
To know more about inverse,
https://brainly.com/question/13593989
#SPJ11
Help plz and thank u!!!!

Answers
Step-by-step explanation:
the answer is 53 :))))))
whats the answer to this question

Answers
Answer:
180 most likely
Neal dropped a small stone off a bridge that is 10m above the water. The height of the stone is given by the function, h(t) = -4.9t2 + t + 10, where h(t) is the height in metres and t is the time in seconds. How long will it take for the stone to hit the water?
Answers
There are two possible values for t: one positive and one negative. However, since time cannot be negative, we only consider the positive value: t ≈ 2.02 seconds; So, it will take approximately 2.02 seconds for the stone to hit the water.
To find out how long it will take for the stone to hit the water, we need to determine when h(t) equals 0 (since the water's surface is considered to be at height 0). We can use the given function: h(t) = -4.9t^2 + t + 10.
Set h(t) to 0 and solve for t:
0 = -4.9t^2 + t + 10
Now, we need to solve this quadratic equation for t. We can do this by applying the quadratic formula:
t = (-b ± √(b^2 - 4ac)) / 2a
In our case, a = -4.9, b = 1, and c = 10. Plugging these values into the formula:
t = (-(1) ± √((1)^2 - 4(-4.9)(10))) / 2(-4.9)
t = (-1 ± √(1 + 196)) / -9.8
t = (-1 ± √197) / -9.8
There are two possible values for t: one positive and one negative. However, since time cannot be negative, we only consider the positive value:
t ≈ 2.02 seconds
So, it will take approximately 2.02 seconds for the stone to hit the water.
Visit here to learn more about quadratic equation : https://brainly.com/question/30098550
#SPJ11
If the area of rectangular plot is 180sq. M and its length is 15m, then its breadth is
Answers
The breadth of the rectangular plot is equal to the area divided by the length. Therefore, the breadth of the plot is 180 divided by 15, which is equal to 12 meters.
The area of a rectangular plot is equal to the length multiplied by the breadth. This means that if the area of the plot is 180 square meters and the length is 15 meters, then the breadth can be calculated by dividing the area by the length. Therefore, the breadth of the plot is 180 divided by 15, which is equal to 12 meters. This means that the area of the plot is equal to 15 multiplied by 12 which is equal to 180 square meters. As the area and the length are given, the breadth can be easily calculated by dividing the area by the length. This is a simple way to calculate the breadth of a rectangular plot when the area and the length are known.
Learn more about rectangle here
https://brainly.com/question/29068457
#SPJ4
A trinomial with a leading coefficient of 3 and a constant term of -5 Choose 1 answer: (A) 3m^(2)+m-5 (B) -5m^(2)+4m+3 (C) 3m^(2)-5m+1 (D) 3m^(2)-5.
Answers
A trinomial is a polynomial with three terms that has a leading coefficient of 3 and a constant term of -5 is
3m²+m-5
Here the degree of the trinomial is 2, so the leading coefficient is the coefficient of the term with m², which is 3.
The constant term is the term without a variable, which is -5
To find the coefficient of middle term of the trinomial, formula is:
coefficient of middle term =
(sum of the coefficients of the first and last terms)
2
The sum of the coefficients of the first and last terms is 3 - 5 = -2.
Dividing by 2, we get -1 as the coefficient of the middle term.
Putting all of this together, we can write the trinomial as: 3m² +m - 5
Learn more about polynomials here:
https://brainly.com/question/11536910
#SPJ11
What are the 3 possible sources of error when performing a kinetics experiment using a spectrophotometer to determine the transmittance of crystal violet concentration with sodium hydroxide?
Answers
The three possible sources of error when performing a kinetics experiment using a spectrophotometer
to determine the transmittance of crystal violet concentration with sodium hydroxide include;
errors due to the instrument itself, errors due to the sample solution, and errors due to the experiment.
The instrument itself, which can be an error source, includes improper calibration of the instrument, inaccuracies in instrument readings, or the presence of stray light.
The second possible source of error is the sample solution.
The sample solution may contain impurities, foreign substances, or air bubbles, all of which can affect the measurement.
The final possible source of error is the experimenter. If the experimenter does not take readings at the appropriate time, use incorrect amounts of chemicals, or not wash the instrument correctly, measurement errors may occur.
Therefore, the experimenter should be cautious in handling the instrument and recording data, and should follow the instructions exactly to minimize errors. The above three possible sources of error are only a few examples that can contribute to inaccuracy in kinetic experiments when using a spectrophotometer.
By identifying these possible errors, the experimenter can take steps to minimize their effects and increase the accuracy of the experiment.
Learn more about spectrophotometer, visit here
https://brainly.com/question/24864511
#SPJ11
Sarah has a cell phone plan that charges $0.12 per minute plus a monthly fee of $21.00. She budgets $65.50 per month for total cell phone expenses without taxes. What is the maximum number of minutes Sarah could use her phone each month in order to stay within her budget?
Answers
Answer:
44.5 minutes on her phone to stay within budget
Step-by-step explanation:
65.50-21.00 = 44.50
44.50x0.12 = 5.34
5.34 divided by 0.12 = 44.5
Find the distance (d) between the planes -5 x-4 y+4 z=42 and -5 x-4 y+4 z=-101 d=
Answers
The distance (d) between the two planes is approximately 5.55 units.
To find the distance (d) between two parallel planes, we can use the formula for the distance between a point and a plane. We need to find a point that lies on one of the planes and calculate the perpendicular distance from that point to the other plane. The normal vector of the planes can be used to determine the perpendicular distance.
In this case, the given planes are -5x - 4y + 4z = 42 and -5x - 4y + 4z = -101. The coefficients of x, y, and z represent the normal vector of the planes.
Taking the normal vector (a, b, c) as (-5, -4, 4) from either of the planes, we can select a point on one of the planes. For simplicity, let's choose the point (0, 0, 0) which lies on both planes.
Now, we can calculate the perpendicular distance (d) between the two planes using the formula:
d = |a*x + b*y + c*z - d| / sqrt(a^2 + b^2 + c^2)
In this case, substituting the values into the formula, we have:
d = |(-5)*(0) + (-4)*(0) + (4)*(0) - 42| / sqrt((-5)^2 + (-4)^2 + 4^2)
= |-42| / sqrt(25 + 16 + 16)
= 42 / sqrt(57)
≈ 5.55
Therefore, the distance (d) between the two planes is approximately 5.55 units.
To find the distance between two parallel planes, we can utilize the concept of a perpendicular distance. Two planes are considered parallel if their normal vectors are parallel. The normal vector is a vector that is perpendicular to the plane and helps define its orientation.
In this problem, we are given two planes: -5x - 4y + 4z = 42 and -5x - 4y + 4z = -101. Notice that the coefficients of x, y, and z are the same in both planes, indicating that they are parallel.
To calculate the distance between these planes, we need to determine the perpendicular distance from one plane to the other. We can achieve this by selecting a point on one of the planes and finding the distance between that point and the other plane.
Choosing the point (0, 0, 0) as it lies on both planes, we can substitute its coordinates into the equation of the second plane (-5x - 4y + 4z = -101) to calculate the perpendicular distance.
Using the distance formula, which involves the coefficients of x, y, and z in the plane equation, as well as the coordinates of the selected point, we can compute the perpendicular distance. The formula takes into account the absolute difference between the two planes' equations and divides it by the magnitude of the normal vector.
By substituting the values into the formula and simplifying, we find that the distance between the two planes is approximately 5.55 units. This means that any point on one plane is approximately 5.55 units away from the other plane in a direction perpendicular to both planes.
Learn more about perpendicular distance here:
brainly.com/question/31658149
#SPJ11
express the number in trigonometric form. -2 + 2 √3 i
Answers
Given:
z = -2 + 2 √3 i
The objective is to write the number in trigonometric form.
The trigonometric form can be represented as,
\(z=r(\cos \theta+i\sin \theta)\)The general form of complex number is, z = x+iy.
By comparing with the given equation.
x = -2
y = 2 √3
The value of r can be calculated as,
\(\begin{gathered} r=\sqrt[]{x^2+y^2} \\ r=\sqrt[]{(-2)^2+(2\sqrt[]{3})^2} \\ r=\sqrt[]{4+4\cdot3} \\ r=\sqrt[]{4+12} \\ r=\sqrt[]{16} \\ r=4 \end{gathered}\)The value of theta can be calculated as,
\(\begin{gathered} \theta=\tan ^{-1}(\frac{y}{x}) \\ \theta=\tan ^{-1}(\frac{2\sqrt[]{3}}{-2}) \\ \theta=\tan ^{-1}(-\sqrt[]{3}) \\ \theta=-^{}60^0 \\ \theta=-\frac{\pi}{3} \end{gathered}\)Now, substitute the obtained values of r and theta in the general equation of trigonometric form.
\(z=4\lbrack\cos (-\frac{\pi}{3})+i\sin (-\frac{\pi}{3})\rbrack\)Since,
\(\begin{gathered} \cos (-\theta)=\cos \theta \\ \sin (-\theta)=-\sin \theta \end{gathered}\)Then,
\(z=4\lbrack\cos \frac{\pi}{3}-i\sin \frac{\pi}{3}\rbrack\)Hence, the required trigonometric form is obtained.
find the area of the region enclosed by one loop of the curve. r = sin(4θ)
Answers
π/16 is the area enclosed by the curve r= sin(4θ)
The given curve is polar curve and hence the area of the polar curve is given by:
Let A be the area of the curve so,
A = \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\)
where a and b is the boundary at which r=0
so after equation r=0
sin(4θ) =0
=> sin(4θ) =0
=> 4θ = 0,π
=> θ = 0, π/4
so a=0 , b= π/4
now
A = \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\) ------(i)
so \(r^2\) = (sin(4θ))^2
=> \(sin^2\)( 4θ )
ans we know that
cos(2α) = 1 - \(2sin^2\)2 α
so \(sin^2\)= (1- cos(8θ) )/2
putting the value of r in the equation (i) we get :-
A = \(\int\limits^b_a {\frac{1}{4} *(1-cos8\theta) } \, d\theta\)
=> 1/4* \(\int\limits^b_a {(1-cos8\theta) } \, d\theta\)
here a=0 and b=π/4
after putting the value and solving the integral
A = π/16
so A is the area enclosed by r=sin(4θ) is π/16
To know more about polar curve click on below link:
brainly.com/question/1094340#
#SPJ4