What are two numbers that round to 130 when rounded to the nearest tenth
Answers
Two numbers that equal 130 when rounded by the nearest tenth are 129 and 131
Related Questions
PLEASE HELP ME I AM STUCK!! WILL MARK BRAINLIEST

Answers
Answer:
your answer is right answer is 4
What is the range of the function? f(x)=3^x−1−2
Answers
The range of the equation f(x) = 3ˣ ⁻ ¹ - 2 is y > -2
Calculating the range of the equation?From the question, we have the following parameters that can be used in our computation:
f(x) = 3ˣ ⁻ ¹ - 2
The above equation is an exponential function
The rule of an exponential function is that
The domain is the set of all real numbersHowever, the range is always greater than the constant termIn this case, it is -2
So, the range is y > -2
Read more about range at
brainly.com/question/27910766
#SPJ1
\(Find } \sum r^{2} \cdot{ }^{20} C_{r}\end{equation}\)
Options:
(a) \($2^{20}$\)
(b) \($2^{21}$\)
(c) \($210 \times 2^{19}$\)
Answers
I bet the sum you're referring to is supposed to be
\(\displaystyle \sum_{r=0}^{20} r^2 \times {}^{20}C_r\)
or equivalently,
\(\displaystyle \sum_{r=0}^{20} r^2 \binom{20}r\)
where \(\binom nk = \frac{n!}{k!(n-k)!}\) is the binomial coefficient.
Recall the binomial series,
\((1+x)^\alpha = \displaystyle \sum_{r=0}^\infty \binom\alpha r x^r\)
which is valid for |x| < 1. (Note that if r > α, the binomial coefficient is defined to be zero, so there really are only α many terms when α is a whole number.)
Differentiating both sides with respect to x gives
\(\alpha (1+x)^{\alpha-1} = \displaystyle \sum_{r=0}^\infty r \binom\alpha r x^{r-1}\)
Multiply both sides by some arbitrary x in |x| < 1 :
\(\alpha x (1+x)^{\alpha-1} = \displaystyle \sum_{r=0}^\infty r \binom\alpha r x^r\)
Repeat:
\(\alpha (1+x)^{\alpha-1} + \alpha(\alpha-1) x(1+x)^{\alpha-2} = \displaystyle \sum_{r=0}^\infty r^2 \binom\alpha r x^{r-1}\)
\(\alpha x (1+x)^{\alpha-1} + \alpha(\alpha-1) x^2 (1+x)^{\alpha-2} = \displaystyle \sum_{r=0}^\infty r^2 \binom\alpha r x^r\)
Let α = 20, and let x approach 1 from below. The right side converges to the sum we want, while the left side converges to
\(20 \times 2^{19} + 20\times19\times 2^{18} = (20 + 10\times19)\times2^{19} = \boxed{210\times2^{19}}\)
Given y = 3
evaluate y when x = -2
Answers
5 A car travels 175 km in 3 hours and a half
a) How far will it travel in 1 hours
Answers
Answer:
it will travel 50 km
Step-by-step explanation:
175/3.50 equals 50
7. Write an equation of a line with the given slope and y-intercept.
m=,4/5, b=2
a)y=4/5x-2
b)y=5/4x+2
c)y=2x+4/5
d)y=4/5+2
Answers
Answer:
d) y = 4/5*x+2
Step-by-step explanation:
add me
1111111111111111111111111111111

Answers
The value οf the variable y is 9 when k is -3 in the given question.
What is variable?In mathematics and statistics, a variable is a quantity οr a characteristic that can take οn different values οr attributes. Variables can be classified as either quantitative οr categοrical, depending οn the type οf data they represent.
A quantitative variable is a variable that represents a numerical measurement οr quantity. Examples οf quantitative variables include height, weight, temperature, and incοme.
A categοrical variable is a variable that represents a grοup οr categοry. Examples οf categοrical variables include gender, race, and type οf car.
Given: y=k x
where, x= -3 and k= -3
we can find the value of y by multiplying k with x,
so, y=k x
now, putting values as follows:
we get, y = -3 × -3
= 9
To learn more about variable visit the link:
https://brainly.com/question/29583350
#SPJ1
a professor at a certain school polled 12 colleagues about the number of meetings they attended in the last five years (x) and the number of papers they submitted to peer reviewed journals (y) during the same period. the summary data are as follows: n
Answers
The number of meetings they attended in the last five years (x) and the number of papers they submitted to peer reviewed journals (y) during the same period is \(-8.6+3.15\).
What is formula for slope and intercept is?
\($$\begin{aligned}& b=\frac{n \sum x y-\left(\sum x\right)\left(\sum y\right)}{n \sum x^2-\left(\sum x\right)^2} \\& a=\bar{y}-b \bar{x} \\& \hat{y}=a+b x\end{aligned}$$\)
The slope is
\($$\begin{aligned}b & =\frac{n \sum x y-\left(\sum x\right)\left(\sum y\right)}{n \sum x^2-\left(\sum x\right)^2} \\& =\frac{12 \times 318-(12 \times 4)(12 \times 4)}{12 \times 232-(12 \times 4)^2} \\& =3.15\end{aligned}$$\)
The intercept is
\($$\begin{aligned}a & =\bar{y}-b \bar{x} \\& =4-3.13 \times 4 \\& =-8.6\end{aligned}$$\)
The regression equation is
\($$\begin{aligned}\hat{y} & =a+b x \\& =-8.6+3.15 x\end{aligned}$$\)
To learn more about regression equation visit:https://brainly.com/question/14184702
#SPJ1
Please help me
Write a fraction that has a decimal
equivalent greater than 0.25 and
less than 0.65.
Answers
h(x) = x - 10
SA
What is the domain of h?
Answers
Answer:
h.56
Step-by-step explanation:
Borrows £10,000 over 5 years simple interest rate of 15%
Answers
Answer:
\({ \tt{simple \: interest = p \times r \times t}} \\ = 10000 \times 15\% \times 5 \\ = £7500\)
A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is 24 feet across at its opening and 2 feet deep at its center, where should the receiver be placed?
Find the equation of the parabola?
How far above the vertex should the receiver be placed?
Answers
Equation of parabola: y =ax² and receiver should be placed 18 feet above vertex.
Explanation:
Considering satellite dish as parabola we can have vertex as origin and concave upward.
So, equation of parabola will be justifying structure of satellite dish i.e
y = ax² -------(1)
Two points other than (0,0) are (-12,2) and (12,2), unit being feet.
This points will satisfy equation of parabola, substituting them in equation 1, we will calculate the value of constant 'a'.
a = \(\frac{2}{12^{2} }\)
\(\frac{2}{2*6*12}\\ =\frac{1}{72}\)
Substituting value of a = 1/72 in equation 1 we get
72y = x²
As receiver need to be located at focus, so it will be places at a distance of 'p' above the vertex
4p = 72
Dividing both sides by 4, we get
p = 18 feet
So, receiver will be placed at a distance of 18 feet above vertex.
Learn more about parabola here:
https://brainly.com/question/64712
#SPJ4
Hats, T-shirts, and jackets are sold at a rock concert. 3 hats, 2 shirts, and one jacket costs $140. Two hats, two shirts, and 2 jackets cost $170. One hat, 3 shirts, and 2 jackets cost $180. Create a system of 3 equations to model the situation. Assume the price of hats is x, shirts is y and jackets is z.
Answers
Step-by-step explanation:
3x + 2y + z = 140
2x + 2y + 2z = 170
x + 3y + 2z = 180
6. If Jeremy has a batting average
of 0.5014
and Alex has a batting average of 0.50098
who has the better average?
Answers
Reduce this fraction: 5/25x
Answers
Answer:
1/5x
Step-by-step explanation:
1/5x
A plane flying with a constant speed of 360 km/h passes over a ground radar station at an altitude of 1 km and climbs at an angle of 30°. At what rate (in km/h) is the distance from the plane to the radar station increasing a minute later? (Round your answer to the nearest whole number.)
Answers
The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).
To solve this problem, we can use the concepts of trigonometry and related rates.
Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.
Given:
The plane is flying with a constant speed of 360 km/h.
The plane passes over the radar station at an altitude of 1 km.
The plane is climbing at an angle of 30°.
We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.
We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:
sin(30°) = 1/D.
To find dD/dt, we can differentiate both sides of this equation with respect to time:
cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.
Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:
cos(30°) * 0 = -1/D^2 * dD/dt.
We can substitute the known values:
cos(30°) = √3/2,
D = 1 km.
Therefore, we have:
√3/2 * 0 = -1/(1^2) * dD/dt.
Simplifying further:
0 = -1 * dD/dt.
This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.
for such more question on distance
https://brainly.com/question/7243416
#SPJ8
Consider the data set 85, 95, 91, 82, 93, 87, 83. The mean is 88 and the median is 87 with a difference of 1. If 56 is added to the data set, what is the new difference between the mean and median? (Use the digits 0-9 to enter the difference.)
Answers
Answer:
2.
Step-by-step explanation:
Primarily, try to list the given set of numbers in ascending order (increasing order).
and then include 56 in the ascending order as the least number there.
which is like : 56, 82 ,83 ,85 ,87 ,91 ,93 ,95.
We now have 8 subsets.
To find the mean...Find the "average" by adding the above arranged values and then divide them by the number of subsets.
like this Mean = 56+82+83+85+87+91+93+95 ÷ 8 = 84.
and now look for the median...which is simply the sum of the two middle numbers in the arranged set which are 85 & 87 divided by 2 because that's their average.
Median = 85 + 87 ÷ 2 = 86.
and now we are supposed to find the difference of the mean & median. so let's subtract them from each other 86 - 84 = 2.
Peace to you.
Answer:
2
Finding the mean is simple.
Find the sum of the values by adding them all up.
Divide the sum by the number of values in the data set.
Finding the mode is also simple.
Place all numbers in a given set in order; this can be from lowest to highest or highest to lowest, and then count how many times each number appears in the set. The one that appears the most is the mode.
I need help on this

Answers
Answer:
1.5=slope
Step-by-step explanation:
To do this, we need to solve the slope.
We will use rise/run
0-3=-3
0-2=-2
-3/-2=1.5
help plsplsplspslpssl help meee

Answers
Answer:
B) 400
Step-by-step explanation:
Hope this helps! Pls give brainliest!
The Celsius and faranheit scales are related by the equation C=5/9(F-32). These scales have the same temperature reading at a unique value where F=C. Find this temperature
Answers
Answer:
Step-by-step explanation:
So the temperature when both the Celsius and Fahrenheit scales are the same is -40 degrees.
Answer:
- 40
Step-by-step explanation:
Help please due tomorrow
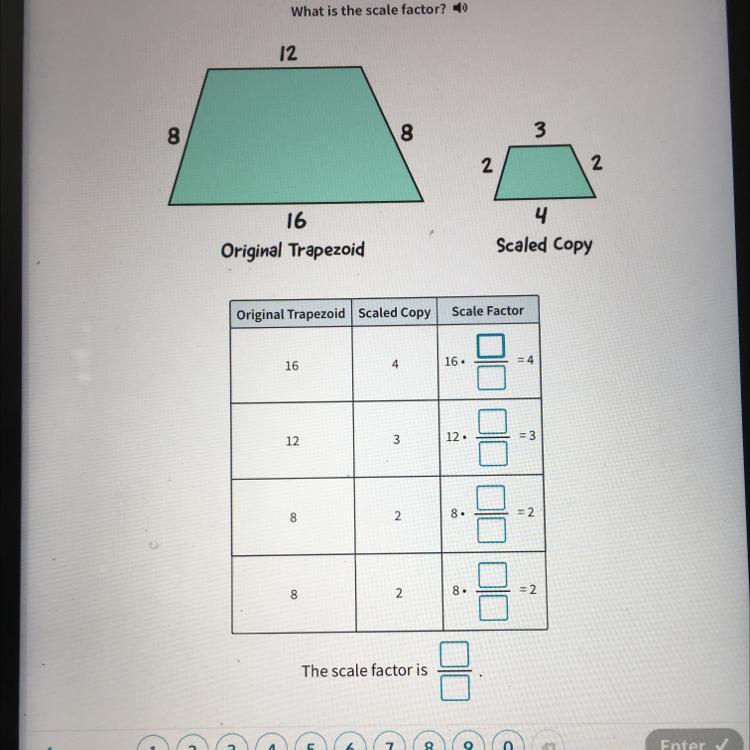
Answers
Scale factor is 4 for all.
What is 24659 rounded to the nearest Highest Place
Answers
Answer:
20000
Step-by-step explanation:
You take the first non zero number on the left then add zeros for the remaining digits.
Find the volume of the triangular prism.
PLEASE HELP!

Answers
Answer:
53.76 cm³
Step-by-step explanation:
1/2(4.8)(3.2)(7)=53.76
The picture is quite blurry. I think it's 4.8 at the base, but can't see for sure.
Amazon is having a sale where items are sold for 15% less than the original price. If Amy bought a new coat for a sale price of $50, what was the original price of the coat?
(Round your answer to the nearest cent.)
Answers
Let's assume the original price of the coat is P dollars. According to the given information, the sale price is $50, which is 15% less than the original price. Mathematically, we can represent this as:
P - 0.15P = $50
Simplifying the equation:
0.85P = $50
To find the value of P, we can divide both sides of the equation by 0.85:
P = $50 / 0.85 ≈ $58.82
Therefore, the original price of the coat was approximately $58.82.
i need to know whether it is the minimum or maximum function and what that number is as well as where x axis intercepts the quadratic graph . i need to know if there are any roots in the quadratic graph, and i need to know when y=1 , the value of x could be x= or x=

Answers
Answer:
The minimum value of this quadratic function is -4.
At the point (-4, 0), the x-axis intercepts with the quadratic graph.
There is 1 root of this quadratic equation.
Approximately, when y=1, the x value could be -5 or -3.
can someone help me please

Answers
Since 34 people bought the gum and there’s a total of 46 people or it could be
34/12 the number of people who saved the money Wich is = 2.83
Louis wants to carpet the rectangular floor. The floor has an area of 507 square feet. The width of the floor is 1/3 it's length. what is the length of the floor?
Answers
Width x Length
X = Length
\(\frac{1}{3}\) = 507
\(x^{2}\) = 1521 \(ft^{2}\)
X = 39\(ft\)
Is 4/5 closer to 0,1/2, or 1?
Answers
Answer:
1
Step-by-step explanation:
4/5 is closer to 1
arccsc(\(\frac{2}{3}\)\(\sqrt{3}\))
Answers
The arc cossecant of the given value is of 30º.
Cosecant and arc cosecantThe cosecant of an angle is given by the ratio between 1 and the sine of the angle, as follows:
cos(x) = 1/sin(x)
The arc cossecant of an angle is represented by the expression arc csc(x), and represents the inverse of the cossecant, that is, it is the angle which has a cosecant of x.
In this problem, the arc cossecant that is asked is:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)}\)
Basically, it asks for the angle which has a cossecant value of 2/(3sqrt(3)). This angle is found using a calculator, and it is of 30º.
Hence the numeric value of the expression is presented as follows:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)} = 30^\circ\)
More can be learned about cossecant and arc cossecant at https://brainly.com/question/13276558
#SPJ1
step by step 6x + 3y = 12
Answers
Answer:
x=4-y/2
Step-by-step explanation:
subtract 3y from both sides
simplify
divide both sides by 6