what is 99,765 divided by 5?
Answers
Answer:
It is 19,953. Your welcome
Answer:
99,765/5= 19953 :)
Step-by-step explanation:
Related Questions
Use your calculator to find the approximate volume in cubic units of the solid created when the region under the curve y = sin(x) on the interval [0, π] is rotated around the x-axis.
Answers
The approximate volume of the solid created by rotating the region under the curve y = sin(x) on the interval [0, π] around the x-axis is approximately 2.094 cubic units.
To find the volume of the solid, we can use the disk method. Considering a small segment on the x-axis between x and x + Δx, the corresponding slice of the solid can be approximated as a disk with radius y = sin(x) and thickness Δx. The volume of this disk is given by V = π * (sin(x))^2 * Δx.
To find the total volume of the solid, we need to sum up the volumes of all the disks. We can do this by taking the limit as the thickness Δx approaches zero and integrating over the interval [0, π]. Thus, the volume can be calculated as V = ∫[0, π] π * (sin(x))^2 dx.
Using a calculator or integration software, we can evaluate this definite integral. The result is approximately 2.094 cubic units. Therefore, the approximate volume of the solid created by rotating the region under the curve y = sin(x) on the interval [0, π] around the x-axis is approximately 2.094 cubic units.
Learn more about volume of the solid here:
https://brainly.com/question/32439212
#SPJ11
Solve me given equation, Enter your answers as a comma-separated list. Let k be any integer. Round terms to two decimal places where appropriate.) cos theta = - 1/2 theta = rad List six specific solutions. theta = rad Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to two decimal places where appropriate.) sin theta = Squareroot 2/2 theta = rad List Six specific solutions. theta = rad Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to two decimal places where appropriate.) cot theta = 0.16 theta = rad List six specific solutions. theta = rad Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to two decimal places where appropriate.) tan theta = -10 theta = rad List six specific solutions. theta = rad
Answers
Solving the given equations:
cos(theta) = -1/2
theta = 2π/3 + 2πk, 4π/3 + 2πk
(Specific solutions: theta = 2π/3, 4π/3, 8π/3, 10π/3, ...)
sin(theta) = √2/2
theta = π/4 + πk, 3π/4 + πk
(Specific solutions: theta = π/4, 3π/4, 5π/4, 7π/4, ...)
cot(theta) = 0.16
theta = arccot(0.16)
theta ≈ 1.41 radians
(Specific solutions: theta ≈ 1.41)
tan(theta) = -10
theta = arctan(-10)
theta ≈ -1.47 radians
(Specific solutions: theta ≈ -1.47)
Learn more about equations from
https://brainly.com/question/17145398
#SPJ11
I need ASAP I Will mark Brainlyest

Answers
Answer:
the answer is D. y > \(-\frac{3}{2}x + 1\)
hope this helps
Find the measure of x.
40
45°
X
x = [?]
X
Round to the nearest tenth.
![Find the measure of x.4045Xx = [?]XRound to the nearest tenth.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/4Ouvx9vQXZc4He557KA2qVtebCwcWIwK.png)
Answers
Answer:
x ≈ 28.3
Step-by-step explanation:
using the cosine ratio in the right triangle
cos45°= \(\frac{adjacent}{hypotenuse}\) = \(\frac{x}{40}\) ( multiply both sides by 40 )
40 × cos45° = x , then
x ≈ 28.3 ( to the nearest tenth )
help :((((((((((((((((((((((((((
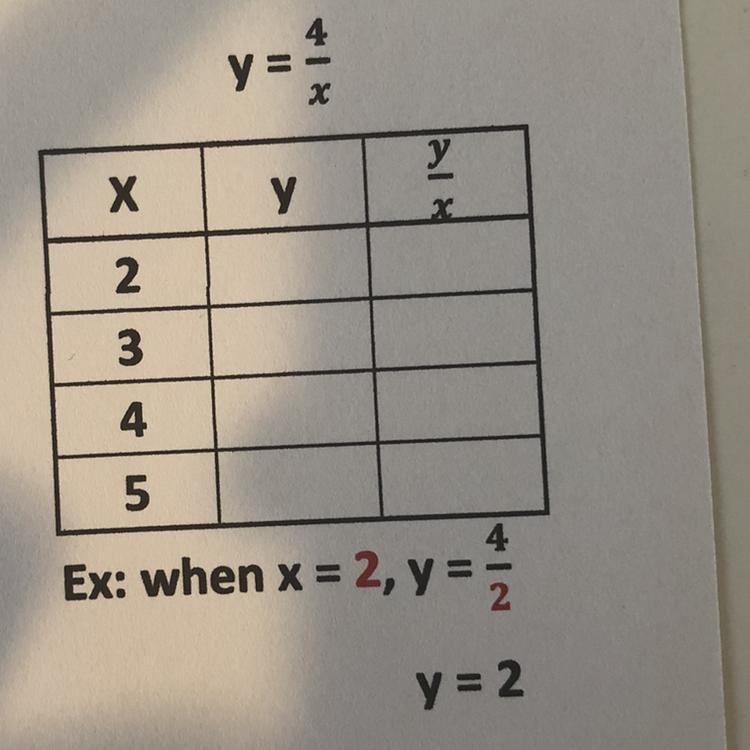
Answers
Y/x for 2 it is 8 for 3 it is 12, 4 is 16 and 5 is 20
1. Let F Be Differentiable Function On R. Suppose That F′(X)=0 For Any X∈R. Prove That F Has At Most One Real Root.
Answers
To prove that a differentiable function F has at most one real root when F'(x) ≠ 0 for any x ∈ R, we can use the intermediate value theorem.
Suppose, by contradiction, that F has two distinct real roots, say a and b, where a ≠ b. Without loss of generality, assume a < b. Since F is differentiable, it is continuous on the closed interval [a, b] and differentiable on the open interval (a, b).
By the mean value theorem, there exists a point c in the open interval (a, b) such that:
F'(c) = (F(b) - F(a))/(b - a)
Since F(a) = F(b) = 0 (since a and b are roots of F), we have:
F'(c) = 0/(b - a) = 0
This contradicts the assumption that F'(x) ≠ 0 for any x ∈ R. Therefore, our initial assumption that F has two distinct real roots is false, and we conclude that F can have at most one real root.
This proves that if a differentiable function F has F'(x) ≠ 0 for any x ∈ R, then F has at most one real root.
To know more about intermediate value theorem refer here:
https://brainly.com/question/30403106
#SPJ11
simplify
6 ÷ 3 + 32 · 4 − 2
Answers
Answer:
128 <33
Step-by-step explanation:
6 ÷ 3 + 32 • 4 - 2 = 128
▪︎▪︎▪︎▪︎▪︎▪︎
Which expression is equivalent to the given expression?
√45
A. 5√9
B. 3√5
C. 9√5
D. 5√3
Answers
First you need to factor: √3^2 • 5
Find the root: √3^2 √5
Simplify: 3√5
Find the value of x (7TH GRADE MATH)

Answers
Answer:
the answer is 5
Step-by-step explanation:
a right angle has a total of 90 degrees
so you subtract 65 from 90 and get 25
that is the total degrees in the rest of the angle
then you would have to divide 25 by 5
leaving you with 5
"Arc Length and Area"
Explanation needed

Answers
we know that a whole circle is found using π\(r^{2}\).
So π\(10^{2}\) = 314
so now we know that the whole circle is 314 squared units, we need to find the specific portion.
Oh wait, i learned this lol,
formula for area of sector
As (areas of sector) = π\(r^{2}\)(\(\frac{θ}{360}\))
As (areas of sector) = π\(10^{2}\)(\(\frac{θ}{360}\))
100 times 3.14
314 (43/360)
314(0.12)
As (areas of sector) = 37.68
I hope this finds you well, and have a great day.
13y-5=9y+27
What is y?
Answers
Answer:
y=8
Step-by-step explanation:
if quick i will give brainlyist
Sandra files folders for her job. According to the graph, how many minutes will it take her to file 100 folders?
A. 10
B. 80
C. 90
D. 100

Answers
Answer:
A its 10
Step-by-step explanation:
Which expression is equivalent to the model? (look in attached image)

Answers
Karim wants to invest $100000 in two investments at 8% and 10%. How much should he invest in each if he wants to obtain an annual income from both investments of $9000?
Answers
Let's denote the amount invested at 8% as x and the amount invested at 10% as y.
According to the given information, Karim wants to invest a total of $100,000, and the combined annual income from both investments should be $9,000.
Set up the equations based on the information:
The first equation represents the total amount invested:
x + y = 100,000
The second equation represents the total annual income from the investments:
0.08x + 0.1y = 9,000
Solve the equations:
We can use the substitution or elimination method to solve the system of equations. Let's use the elimination method:
Multiply the first equation by 0.08 to match the coefficients of x:
0.08x + 0.08y = 8,000
Now subtract this equation from the second equation to eliminate x:
(0.08x + 0.1y) - (0.08x + 0.08y) = 9,000 - 8,000
0.02y = 1,000
Divide both sides of the equation by 0.02:
y = 1,000 / 0.02
y = 50,000
Substitute the value of y back into the first equation to solve for x:
x + 50,000 = 100,000
x = 100,000 - 50,000
x = 50,000
Calculate the amounts to invest:
Karim should invest $50,000 at 8% and $50,000 at 10% in order to obtain an annual income of $9,000 from both investments.
Karim should invest $50,000 at 8% and $50,000 at 10% in order to obtain an annual income of $9,000 from his investments.
To know more about elimination method, visit
https://brainly.com/question/13877817
#SPJ11
• write each answer in simplest form.
1. 1/6 +2/6
2. 2/5 - 1/5
Answers
Answer:
1. 1/2
2. 1/5
Step-by-step explanation:
I used a calculator!
Answer:
1.3/6 or 1/2
2.1/5
Step-by-step explanation:
Just write that out, thats all the steps there is, 3/6 simplifies to 1/2 because they're equivalent
: (60'+1242-15a)+(4a2-12a+8)
Answers
Answer:
=4a^2 +-27a + 1310

Sixty-four percent of voters in a very large electorate support candidate Smith in an upcoming election. A student employee working the evening shift at a telephone survey facility calls voters at random and asks them which candidate they prefer. a. What is the probability that, among five voters the student calls, exactly one supports candidate Smith? b. What is the probability that, among five voters the student calls, at least one supports candidate Smith? c. What is the probability that the first voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach the first voter who supports candidate Smith? d. What is the probability that the third voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach three voters who supports candidate Smith?
Answers
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4
\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5
\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls. The calculation results in approximately 0.369, or 36.9%.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
[P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
[P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
which family of function does the graph on the right belongs to?
A. trigonometric
B. logarithmic
C. exponential
D. retional
Answers
Answer:
wheres the graph
Step-by-step explanation:
A) trigonometric or D) retional
Hope that helps, I’m between those two checks which one is the right answer :)
What is the solution to:
\( \frac{5}{8} = \frac{m}{12} \)
HELP! answer if you can.
Answers
Answer:
\(\boxed{m=7.5}\)
Step-by-step explanation:
Hey there!
Cross multiply the given info
60 = 8m
Divide both sides by 8
m = 7.5
Hope this helps :)
Last summer, Jon’s family found 152 shells at the beach. This summer they were at the beach for 7 days. Each day they found 9 shells. How many fewer shells did they find this year than last year?
Answers
Answer:
Step-by-step explanation:
Since on each day 9 shells were found, and there are 7 days: 7 x 9 = 63
Number of shells found this summer: 63
Number of shells found fewer this year than last year: 152 - 63 = 89
Hence, Jon’s family found 63 fewer shells than last year
Jon’s family found 63 fewer shells than last year if last summer, Jon’s family found 152 shells at the beach. This summer they were at the beach for 7 days.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has a basic four operators that is +, -, ×, and ÷.
It is given that:
Last summer, Jon’s family found 152 shells at the beach. This summer they were at the beach for 7 days.
Let x be the number of shells they find this year than last year.
The value of x can be found as follows:
x = 152 - 7×9
x = 152 - 63
x = 89 shells
Thus, Jon’s family found 63 fewer shells than last year if last summer, Jon’s family found 152 shells at the beach. This summer they were at the beach for 7 days.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ2
PLEASE I NEED THE ANSWER LIKE IN THE NEXT 10 MINS!!!!!
What is f(-2) of the function given below? F(x)=3x^2-4x+1
Answers
Answer: F=(x-1) (3x-1/x =21
Step-by-step explanation: Fx/x=3x^2-4x+1/x
Complete the inequality. 13/18___ 11/14 < > =
Answers
Answer:
Your answer is <, Hope it helps.
Anna baked 3 batches of cookies with c cookies in each batch. She then ate 8 cookies!
Answers
Answer:
\(t=3c-8\)
Step-by-step explanation:
It seems like your question is incomplete, so I will assume it is asking for an expression that represents how many cookies Anna has left.
Let t represent the total number of cookies left. Let's build this expression. If each batch contains c cookies, and there are 3 batches, the total number of cookies baked is 3 times c. Since she ate 8 cookies, 8 must be subtracted from that total. Therefore:
\(t=3c-8\)
Hope this helps!
Solve −2|m|= −10.
What is m?
Answers
Answer:
|m| : -5Step-by-step explanation:
{ -2|m|= -10= |m| : -5 }37:53 Bok Suppose that x has a binomial distribution with n=202 and p= 0.44. (Round np and n(1-p) answers to 2 decimal places. Round your answers to 4 decimal places. Round z values to 2 decimal place
Answers
The mean (µ) and standard deviation (σ) of the binomial distribution with n=202 and p=0.44 are 88.88 and 7.8959, respectively. The probability of obtaining x=53 is approximately 0.0561, and the z-score for x=37 is -6.55.
To find the mean (µ) and standard deviation (σ) of the binomial distribution, we use the formulas µ = np and σ = sqrt(np(1-p)), where n is the number of trials and p is the probability of success.
Given n = 202 and p = 0.44, we can calculate the mean and standard deviation as follows:
µ = 202 * 0.44 = 88.88 (rounded to 2 decimal places)
σ = sqrt(202 * 0.44 * (1 - 0.44)) = 7.8959 (rounded to 4 decimal places)
Now, let's suppose we want to find the probability of obtaining a specific value of x, let's say x = 53. We can use the formula for the binomial probability:
\(P(x) = C(n, x) * p^x * (1 - p)^{n - x}\)
Substituting the values, we have:
\(P(53) = C(202, 53) * (0.44)^{53} * (1 - 0.44)^{202 - 53}\)
Using a binomial calculator or software, we can find the probability as approximately 0.0561 (rounded to 4 decimal places).
Finally, if we want to calculate the z-score for a given value of x, we can use the formula:
z = (x - µ) / σ
For x = 37, the z-score would be (37 - 88.88) / 7.8959 = -6.55 (rounded to 2 decimal places).
In conclusion, for a binomial distribution with n = 202 and p = 0.44, the mean is 88.88 and the standard deviation is 7.8959. The probability of obtaining x = 53 is approximately 0.0561. The z-score for x = 37 is -6.55.
To learn more about Standard deviation, visit:
https://brainly.com/question/475676
#SPJ11
Diane made 4 identical necklaces, each having beads and a pendant. The total cost of the beads and pendants for all 4 necklaces was $23.20. If the beads cost $2.90 for each necklace, how much did each pendant cost?
Answers
Answer:
what is the difference in length and the shortest length
Let h(x)=5+f(x)8g(x) Suppose that f(2)=−4,f (2)=2,g(2)=−1, and g ′ (2)=3. Find h′ (2). Find the values of a and b so that the parabola y=ax 2 +bx has a tangent line at (1,−2) with equation y=4x−6 Find an equation of the tangent line to the curve y=tan 2(x) at the point (π/4,1). Put your answer in the form y=mx+b, and then enter the values of m and b in the answer box below (separated with a comma).
Answers
The equation of the tangent line is y = 2x - π/2 + 1, and the values of m and b are 2 and -π/2 + 1, respectively. To find h'(2), we need to apply the product rule and chain rule. Given that h(x) = 5 + f(x)8g(x), we have:
h'(x) = f'(x)8g(x) + f(x)(8g'(x))
Substituting the values f(2) = -4, f'(2) = 2, g(2) = -1, and g'(2) = 3, we can evaluate h'(2):
h'(2) = f'(2)8g(2) + f(2)(8g'(2))
= (2)(8)(-1) + (-4)(8)(3)
= -16 - 96
= -112
Therefore, h'(2) = -112.
To find the values of a and b for the parabola y = ax^2 + bx, we need to find the slope of the tangent line at (1, -2). The slope of the tangent line is equal to the derivative of the function at that point. So:
y' = 2ax + b
At x = 1, the slope is 4:
4 = 2a + b
Since the tangent line passes through (1, -2), we can substitute these values into the equation:
-2 = a(1)^2 + b(1)
-2 = a + b
We now have a system of equations:
2a + b = 4
a + b = -2
By solving this system, we find a = -6 and b = 4.
Therefore, the values of a and b are -6 and 4, respectively.
To find the equation of the tangent line to the curve y = tan^2(x) at the point (π/4, 1), we need to find the derivative of the function and evaluate it at x = π/4. The derivative of y = tan^2(x) is:
y' = 2tan(x)sec^2(x)
At x = π/4, the slope is:
m = 2tan(π/4)sec^2(π/4)
= 2(1)(1)
= 2
Since the tangent line passes through (π/4, 1), we can use the point-slope form of a line to find the equation:
y - 1 = 2(x - π/4)
Simplifying, we get:
y = 2x - π/2 + 1
Therefore, the equation of the tangent line is y = 2x - π/2 + 1, and the values of m and b are 2 and -π/2 + 1, respectively.
Learn more about tangent line here:
https://brainly.com/question/28994498
#SPJ11
The midsegment of a trapezoid is a segment whose _____ are the midpoints of the legs of a trapezoid.
Answers
Answer:Joints
Step-by-step explanation:
It is likely the joining point so it is so help ful
We will flip a balanced coin 3 times and for each toss, record whether we get a Head or a Tail. Write all possible outcomes of this experiment to find the probability that we get exactly 2 heads. 3/8 2/3 1/8 1/3
Answers
The probability of getting exactly 2 heads when flipping a balanced coin 3 times is 3/8.
When flipping a coin, each flip has 2 possible outcomes: Head (H) or Tail (T). Since we are flipping the coin 3 times, the total number of possible outcomes is 2 × 2 × 2 = 8. To find the probability of a specific outcome, we divide the number of favorable outcomes by the total number of possible outcomes. In this case, the favorable outcomes are the 3 outcomes with exactly 2 heads, and thus the probability is 3/8.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
Simplify the expression.
768x^8y^5
O A. 42³y32²
O B. 2xy² √2x
OC. 4x²y3y
O D. 4x²y3x²y

Answers
Answer:
4y^4√3x^2y
Step-by-step explanation:
Simplify the radical by breaking the radicand up into a product of known factors, assuming positive real numbers.