What is the solution to -4(8 - 3x) 6x - 8?
Help
Answers
Answer:
-40+ 72x
Step-by-step explanation:
-32+12x ×6x-8
-32-8 +12x× 6x
-40 +72x
=72x^2 - 192x - 8
Related Questions
A circular tabletop is to be cut from a rectangular piece of wood that measures 1.20m by 1.80m what is the radius of the largest tabletop that could be cut?
Answers
Answer:
0.6 m
Step-by-step explanation:
From the question,
The largest table top that could be cut from a rectangular piece of wood,
will have a diameter equal to the smallest dimension of the rectangular piece of wood. As shown in the diagram attached.
If it is cut along the biggest dimension of the rectangular piece of wood, the tabletop won't be circular, rather, it will form a sphere. So the only way the tabletop can be cut out of the rectangular piece of wood to make it circular is to cut it along the smaller dimension of the rectangular piece of wood.
Given, the dimensions of the rectangular piece of wood as 1.2 m by 1.8 m.
Then the diameter of the table top formed = 1.2 m.
but,
radius = diameter/2
radius = 1.2/2
radius = 0.6 m
Hence, the radius of the largest tabletop that could be cut out of the rectangular piece of wood is 0.6 m

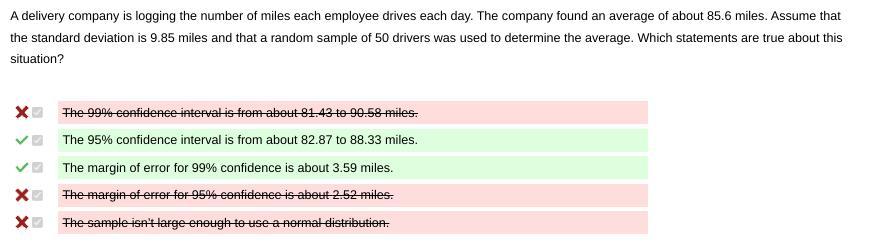
A delivery company is logging the number of miles each employee drives each day. The company found an average of about 85.6 miles. Assume that the standard deviation is 9.85 miles and that a random sample of 50 drivers was used to determine the average. Which statements are true about this situation?
The 99% confidence interval is from about 81.43 to 90.58 miles.
The 95% confidence interval is from about 82.87 to 88.33 miles.
The margin of error for 99% confidence is about 3.59 miles.
The sample isn’t large enough to use a normal distribution.
The margin of error for 95% confidence is about 2.52 miles.
Answers
Answer:
B. The 95% confidence interval is from about 82.87 to 88.33 miles.
C. The margin of error for 99% confidence is about 3.59 miles.
Step-by-step explanation:
No cheese detected or anything hehehe
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
I’ll pay $20 in cashapp for whoever can do this

Answers
Answer:
10
Step-by-step explanation:
What is the range of the function? f(x)=3^x−1−2
Answers
The range of the equation f(x) = 3ˣ ⁻ ¹ - 2 is y > -2
Calculating the range of the equation?From the question, we have the following parameters that can be used in our computation:
f(x) = 3ˣ ⁻ ¹ - 2
The above equation is an exponential function
The rule of an exponential function is that
The domain is the set of all real numbersHowever, the range is always greater than the constant termIn this case, it is -2
So, the range is y > -2
Read more about range at
brainly.com/question/27910766
#SPJ1
Pythagorean theorem - Missing sides
Pls help me I need your help to my homework
If you help me, I help you too I promise

Answers
C is the hypotenuse, and a and b are the other sides of the triangle. You can identify the hypotenuse of the triangle as it being the longest side, and the one opposite the right angle.
I see you have done Question 1 and Question 2 correctly, so I’ll start with Question 3.
(But with question 1, you did the working out slightly wrong but still managed to get the right answer?! That confuses me, but well done!)
Question 3:
The hypotenuse is 4 and the other side length is 3. You can tell the side length that’s 4 is the hypotenuse because it’s the longest side, and the one opposite the right angle.
a^2+b^2=c^2 (c is the hypotenuse)
a^2+3^2=4^2
So: a^2=4^2-3^2
a^2=16-9
a^2= 7
a= root of 7, or 2.6 to one decimal place.
Answer: 2.6 (to one decimal place)
Question 5:
12 is the hypotenuse and 5 is another side length.
a^2+b^2= c^2
a^2+5^2=12^2
So: a^2= 12^2-5^2
a^2= 144-25
a^2= 119
a= root of 119, or 10.9 to one decimal place
Answer: 10.9 (to one decimal place)
I’ll skip question 5, and cover question 6:
Question 6:
This time the side lengths are 5 and 2, and the hypotenuse is missing.
a^2+b^2=c^2
5^2+2^2=c^2
25+4=c^2
29=c^2
c= root of 29, or 5.4 to one decimal place
Answer: 5.4 (to one decimal place)
Try to do the rest of the homework by yourself, with this to help you! (Unless someone else finishes the rest for you)
If you want to get better at something, you have to practice lots, which is why I’m not doing all of it.
(sorry if I’m wrong on any!!)
:)
What is the probability of spinning Green and rolling a 5? PLS HELP 80 POINTS

Answers
Answer:
1/30
Step-by-step explanation:
all of the colours have same probability of being spun. 5 colours.
So, P(spinning a green) = 1/5.
6 sided to a die.
So, P(rolling a 5) = 1/6
P(spinning a green AND rolling a 5) = (1/5) X (1/6) = 1/30
A bank loaned out 20,500, part of it at the rate of 9% annual interest, and the rest at 11% annual interest the total interest earned for both loans was 2,225.00 how much was loaned at each rate
Answers
The money loaned at 9% annual interest was 1500 and the money loaned at 11% annual interest was 19000.
Let the amount of money loaned at 9% be x
the amount of money loaned at 11% be y
According to the question,
Total money loaned = 20,500
Thus the equation formed is,
x + y = 20,500 ------ (i)
Simple interest is calculated by
I = P * r * t
where I is the simple interest
r is the rate of interest
t is the time
Thus, the interest on x = 0.09x
the interest on y = 0.11y
Total interest gained = 2,225
Thus the equation formed is,
0.09x + 0.11y = 2225 -------(ii)
Multiply (i) by 0.09
0.09x + 0.09y = 1845
Subtract the above from (ii)
0.02y = 380
y = 19000
x = 1500
Learn more about Equation:
https://brainly.com/question/28871326
#SPJ1
if the smaller side of a rectangle was increased by 7 cm, it would be exactly 55% of the 110 cm longer side. Find the area of the rectangle
Answers
Answer:
5886 cm
Step-by-step explanation:
start by finding 55% of 110 which is 60.5. then subtract by 7 and then you get 53.5
then multiply 53.5 by 110 = 5885 cm
PLS HELP ME !!!!!!!!!!!!!!!!

Answers
Answer:
C
Step-by-step explanation:
All sides make a cube
Answer:
D
Step-by-step explanation:

Find the value of this expression if x=-9.
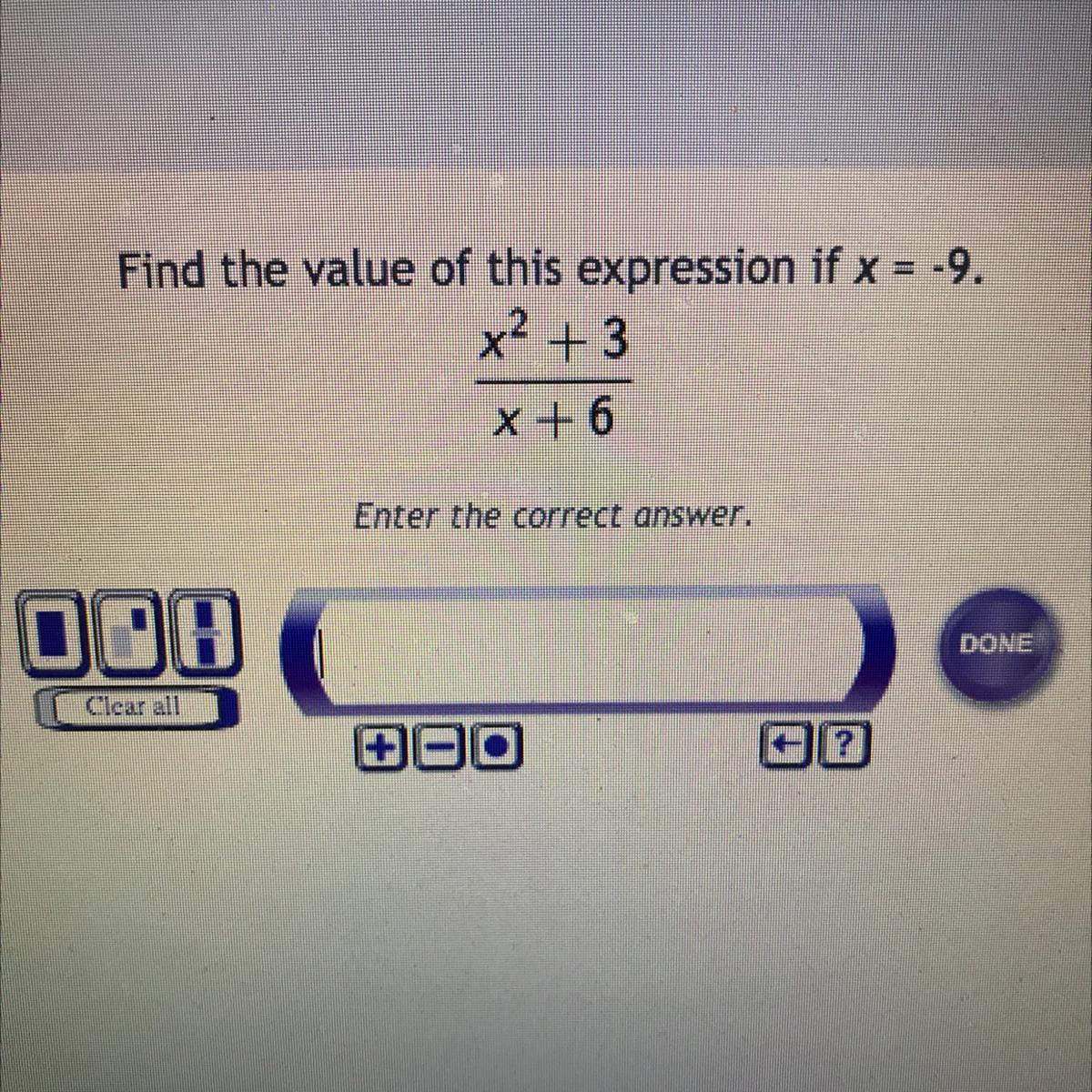
Answers
Answer:
if x = -9
then, (-9)×(-9) + 3
= 81 +3
= 84
(-9) + 6
= -3
so, ans is = 84/(-3)
= (-84)/3
Solve the equation: x²-2x=8
Show all the Steps with explanation.
Answers
Answer:
x = 4, -2
Step-by-step explanation:
x^2-2x=8
Move the constant term to the right side of the equation.
x^2 - 2x = 8
Take half of the coefficient of x and square it.
(-2/2)^2 = 1
Add the square to both sides of the equation.
x^2 - 2x + 1 = 8 + 1
Factor the perfect square trinomial.
(x - 1)^2 = 9
Take the square root of both sides of the equation.
x-1=\(\sqrt{9}\)
x-1=±3
Isolate x to find the solutions.
Taking positive
x=3+1=4
x=4
Taking negative
x=-3+1
x=-2
The solutions are:
x = 4, -2
Answer:
\(x = -2,\;\;x=4\)
Step-by-step explanation:
To solve the quadratic equation x² - 2x = 8 by factoring, subtract 8 from both sides of the equation so that it is in the form ax² + bx + c = 0:
\(x^2-2x-8=8-8\)
\(x^2-2x-8=0\)
Find two numbers whose product is equal to the product of the coefficient of the x²-term and the constant term, and whose sum is equal to the coefficient of the x-term.
The two numbers whose product is -8 and sum is -2 are -4 and 2.
Rewrite the coefficient of the middle term as the sum of these two numbers:
\(x^2-4x+2x-8=0\)
Factor the first two terms and the last two terms separately:
\(x(x-4)+2(x-4)=0\)
Factor out the common term (x - 4):
\((x+2)(x-4)=0\)
Apply the zero-product property:
\(x+2=0 \implies x=-2\)
\(x-4=0 \implies x=4\)
Therefore, the solutions to the given quadratic equation are:
\(\boxed{x = -2,\;\;x=4}\)
Which of the following have a value equal to |37|? Select all that apply.
A. –37
B. |–37|
C. 0
D. –(–37)
E. 37
Answers
Answer:
B, D, and E are the correct answers
Step-by-step explanation:
B, D and E
Hope it helps!!
What is this? I’m too dumb.

Answers
Answer:
its 35
Step-by-step explanation:
y = 6
and 6 times 6 is 36
and 36 minus 1 is 35
:)
Please convert this thank you math experts

Answers
Answer:
1. 55.5
2. 54.5
Step-by-step explanation:
Use division to convert the fraction to a decimal:
1/4 = 1 ÷ 4 = 0.25
Multiply by 100 to get percent value:
0.25 × 100 = 25%
Answer:
1. 0.56
percentage: 56%
2. 0.55
percentage: 55%
Step-by-step explanation:
5/9 to decimal= 0.56
to percentage multiply by 100
same for the second one
Given f(x) and g(x) = f(x) + k, use the graph to determine the value of k.

Answers
Answer:
k = 3
Step-by-step explanation:
The value of k is the amount by which the function f(x) is translated upward to give the function g(x). We can compare y-intercepts to see that the y-intercept of g(x) is 5 -2 = 3 units more than the y-intercept of f(x). This means ...
g(x) = f(x) +3
Comparing to ...
g(x) = f(x) +k
we see that k = 3.
g The manager of a grocery store has selected a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the checkout time is 1 minute. Refer to Exhibit 8-2. The 95% confidence interval for the average checkout time for all customers is _____. a. 2.804 to 3.196 b. 1.04 to 4.96 c. 1.36 to 4.64 d. 3 to 5
Answers
Answer:
The right solution is "0.196".
Step-by-step explanation:
The given values are:
Standard deviation,
\(\sigma=1 \ minute\)
Sample size,
\(n=100\)
Confidence level,
\(c=95\)%
\(=0.95\)
Now,
For \(\alpha=1-c\)
\(= 1-0.95\)
\(=0.05\)
then,
\(Z_{\frac{\alpha}{2} } = Z_{\frac{0.05}{2} }\)
\(=Z_{0.025}\)
\(=1.96\)
The margin or error will be:
⇒ \(E=Z_{\frac{\alpha}{2} } (\frac{\sigma}{\sqrt{n} })\)
On substituting the values, we get
= \(1.96(\frac{1}{\sqrt{100} })\)
= \(1.96\times \frac{1}{10}\)
= \(0.196\)
A spinner has
20
equally sized sections,
2
of which are red and
18
of which are yellow. The spinner is spun and, at the same time, a fair coin is tossed. What is the probability that the spinner lands on yellow and the coin toss is heads?
Do not round your answer.
Answers
The probability that the spinner lands on yellow and the coin toss is heads is 9/20.
To find the probability that the spinner lands on yellow and the coin toss is heads, we need to determine the probability of each event and then multiply them together.
The probability of the spinner landing on yellow is given by the number of yellow sections (18) divided by the total number of sections (20). Therefore, the probability of the spinner landing on yellow is 18/20 or 9/10.
The probability of the coin toss resulting in heads is 1/2 since there are two equally likely outcomes, heads and tails.
To find the probability of both events occurring together, we multiply the individual probabilities:
Probability (Spinner lands on yellow and Coin toss is heads) = Probability (Spinner lands on yellow) * Probability (Coin toss is heads)
= (9/10) * (1/2)
= 9/20
Therefore, nine out of twenty times, the spinner will fall on yellow and the coin will come up heads.
Learn more about probability on:
https://brainly.com/question/23417919
what is 4x+3=11 what is the value of x?
Answers
Answer:
The Answer is x=2
Step-by-step explanation:
Hope this helps!!!!
Answer:
x=2
Step-by-step explanation:
4x+3=11
4x=11-3 ( subtract 3 on both sides)
4x=8
x=2 ( divide 4 on both sides)
Please Help!! (brainliest fr best answer)
1. What is the measure of ∠E? Explain how you know.
2. Describe the relationship between ∠E and ∠K. What is the measure of ∠K?
(image below)
Answers
1. The measure of ∠E = 135°. 2. Angles ∠E and ∠K are alternate exterior angles, and the measure of ∠K = 135°
What is the Exterior Angle?An exterior Angle is defined as an angle produced on the outside of a polygon by extending the sides of the polygon.
The figure is given in the question, as shown.
Since we have a regular octagon that has :
∠I = 45° = ∠G = 45°
Here ∠G + ∠H = 90° (complementary angles)
45° + ∠H = 90°
∠H = 45°
So ∠H + ∠E = 180° (supplementary angles)
45° + ∠E = 180°
∠E = 135°
2. Here the relationship between angles ∠E and ∠K is that they are alternate exterior angles.
So the measure of ∠K = 135°
Learn more about the exterior angles here :
https://brainly.com/question/28835566
#SPJ1
The missing figure has been attached below.

100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
(A) Triangle ABC, and triangle QPR are similar based on side-side-side (SSS) similarity.
(B) Triangle ABC and triangle DEF are similar based on side-side-side (SSS) similarity.
(C) ) Triangle STU and triangle JPM are similar based on side-angle-side (SAS) similarity.
(D) ) Triangle SMK and triangle QTR are similar based on angle-angle (AA) similarity.
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths.
The triangle similarity criteria are:
AA (Angle-Angle)SSS (Side-Side-Side)SAS (Side-Angle-Side)(A) Triangle ABC, and triangle QPR are similar based on side-side-side similarity.
12/8 = 9/6
1.5 = 1.5
(B) Triangle ABC and triangle DEF are similar base on side-side-side similarity as shown in the side lengths.
(C) ) Triangle STU and triangle JPM are similar base on side-angle-side similarity.
14/10 = 21/15
1.4 =
(D) ) Triangle SMK and triangle QTR are similar base on angle-angle similarity.
SMK = 90⁰, 60⁰, 30⁰
QTR = 90⁰, 30⁰, 60⁰
Learn more about similar triangles here: brainly.com/question/27996834
#SPJ1
Need this answered as soon as possible please!! Flo is designing a rectangular billboard using a scale drawing. the billboard is 6 m long. Flo draws a rectangle 12 cm long. The area of Flo's rectangle is 72 cm squared. What is the area of the billboard in square meters?
Answers
Jane's family divided up their garden so that 3/4 of the garden will have vegetables. Jane and her sister will plant 3/4 of the vegetable portion of their garden. How much of the family will Jane and her sister plant?
Answers
9/16 of the family garden
We can use an equation to solve this:
(3/4) * (3/4) = (9/16)
assuming equal population standard deviations for the two groups, give a 95% confidence interval for the
Answers
Answer: Give more info pls
Step-by-step explanation:
The equation Y= X^2/2 - 8 and Y= 2X -2 are graphed below what are the solutions to the equation X^2/2 - 8 = 2X -2 
Answers
The equation X^2/2 - 8 = 2X - 2 has two solutions, X = 6 and X = -2. These are the values of X that satisfy the equation and make both equations Y = X^2/2 - 8 and Y = 2X - 2 intersect on the graph.
To find the solutions to the equation X^2/2 - 8 = 2X - 2, we need to set the two equations equal to each other and solve for X.
The equation is:
X^2/2 - 8 = 2X - 2
To simplify the equation, let's multiply both sides by 2 to eliminate the fraction:
X^2 - 16 = 4X - 4
Next, we rearrange the equation to have all terms on one side:
X^2 - 4X - 12 = 0
Now, we can solve this quadratic equation by factoring, completing the square, or using the quadratic formula. Let's use factoring in this case:
(X - 6)(X + 2) = 0
Setting each factor equal to zero gives us two possible solutions:
X - 6 = 0 --> X = 6
X + 2 = 0 --> X = -2
So the solutions to the equation X^2/2 - 8 = 2X - 2 are X = 6 and X = -2.
For more such question on intersect . visit :
https://brainly.com/question/30915785
#SPJ8
A neighborhood is trying to set up school carpools, but they need to determine the number of students who need to travel to the elementary school (ages 5-10), the middle school (ages 11-13), and the high school (ages 14-18). A histogram summarizes their findings:
Histogram titled Carpool, with Number of Children on the y axis and Age Groups on the x axis. Bar 1 is 5 to 10 years old and has a value of 3. Bar 2 is 11 to 13 years old and has a value of 7. Bar 3 is 14 to 18 years old and has a value of 4.
Which of the following data sets is represented in the histogram?
{3, 3, 3, 7, 7, 7, 7, 7, 7, 7, 4, 4, 4, 4}
{5, 10, 4, 11, 12, 13, 12, 13, 12, 11, 14, 14, 19, 18}
{5, 6, 5, 11, 12, 13, 12, 13, 14, 15, 11, 18, 17, 13}
{3, 5, 10, 11, 13, 7, 18, 14, 4}
Answers
The correct answer is that the data set {3, 7, 4} is represented in the given histogram.(option-a)
The given histogram represents the number of children in each age group who need to travel to school. Since the histogram has only three bars, we can conclude that there are only three age groups.
The first bar represents children aged 5-10, of which there are 3. The second bar represents children aged 11-13, of which there are 7. The third bar represents children aged 14-18, of which there are 4.
Therefore, the data set that is represented in the histogram is:
{3, 7, 4}
None of the other data sets given match the values in the histogram. The first data set has duplicate values and is not sorted by age group. The second data set includes ages that are not represented in the histogram. The third data set has values for ages 6, 11, 12, 13, 14, 15, 17, and 18, but the histogram does not have bars for all those ages. (option-a)
For such more questions on histogram
https://brainly.com/question/32761368
#SPJ8
What is the value of S4 for
♾️. n-1
Σ 1/4(-1/3)
Answers
The value of S4 for the given expression ♾️. n-1 Σ 1/4(-1/3) is -1/12.
The given expression ♾️. n-1 Σ 1/4(-1/3) represents a summation of the term 1/4(-1/3) over a range of values from 1 to n-1, where n is an unknown value. We need to find the value of S4, which represents the sum of this expression when n is equal to 4.
To find the value of S4, we substitute n = 4 into the expression and evaluate it.
♾️. n-1 Σ 1/4(-1/3) = ♾️. 4-1 Σ 1/4(-1/3)
Simplifying, we get:
♾️. 3 Σ 1/4(-1/3)
Since the term 1/4(-1/3) is constant, we can pull it out of the summation:
1/4(-1/3) ♾️. 3
Now, ♾️. 3 represents the sum of 3 terms. Multiplying 1/4(-1/3) by 3 gives:
1/4(-1/3) * 3 = -1/4 * 1/3 * 3 = -1/12
Therefore, the value of S4 for the given expression ♾️. n-1 Σ 1/4(-1/3) is -1/12.
For more such questions on expression, click on:
https://brainly.com/question/1859113
#SPJ8
The probable question could be:
What is the value of s4 for expression ♾️. n-1 Σ 1/4(-1/3) ?
A) 1/9
B) 7/54
C) 5/27
D) 10/27
Fwam and Eva are both driving along the same highway in two different cars to a stadium in a distant city. At noon, Fwam is gar miles away from the stadium and Eva is 396 miles away from the stadium. Fwam is driving along the highway at a speed of 42 miles per hour and Eva is driving at speed of 65 miles per hour. Let F represent Fwam's distance, in miles, away from the stadium t hours after noon. Let E represent Eva's distance, in miles, away from the stadium t hours after noon. Write an equation for each situation, in terms of t, and determine how far both Fwam and Eva are from the stadium at the moment they are an equal distance from the stadium.
Answers
Fwam and Eva are an equal distance of 69 miles away from the stadium when the time t = 3 hours
Given data ,
The formula for the distance (F) of Fwam from the stadium is:
F(t) = 327 - 42t
Since Fwam is travelling at a 42 mph pace, his distance from the stadium is reducing at a 42 mph rate.
The formula for Eva's separation from the stadium is:
E(t) = 396 - 65t
Eva's distance from the stadium also shrinks at a pace of 65 miles per hour as she drives at a speed of 65 mph.
Set F(t) = E(t) and solve for t to get the time at which Fwam and Eva are equally far from the stadium
On simplifying the equations , we get
327 - 42t = 396 - 65t
Adding 65t to both sides:
65t + 327 - 42t = 396
23t + 327 = 396
Subtracting 327 from both sides:
23t = 396 - 327
23t = 69
Dividing both sides by 23:
t = 69 / 23
t = 3 hours
Hence , at t = 3 hours after noon, both Fwam and Eva are an equal distance of 69 miles away from the stadium.
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
The complete question is attached below :
Fwam and Eva are both driving along the same highway in two different cars to a stadium in a distant city. At noon, Fwam is gar miles away from the stadium and Eva is 396 miles away from the stadium. Fwam is driving along the highway at a speed of 42 miles per hour and Eva is driving at speed of 65 miles per hour. Let F represent Fwam's distance, in miles, away from the stadium t hours after noon. Let E represent Eva's distance, in miles, away from the stadium t hours after noon. Write an equation for each situation, in terms of t, and determine how far both Fwam and Eva are from the stadium at the moment they are an equal distance from the stadium.

1. How many multiples of 5 are there in between 14 and 345?
Answers
Answer:
Step-by-step explanation:
66
5 Signs for science project displays are cut of poster board that measure 1 yard on each side. Each sign is-yard long and-yard wide. How ma signs can be cut from 1 piece of poster board? Wh the area of each sign? Show your work.
Answers
Answer:
\(\text{27}\)
Step-by-step explanation:
Given that :
\(\text{Dimension of poster board} = 1 \ \text{yd} \ \text{by} \ 1 \ \text{yd}\)
\(\text{Dimension of each poster board} = \dfrac{1}{3} \ \text{yd} \ \text{by} \ \dfrac{1}{9} \ \text{yd}\)
Number of poster signs that can be cut :
\(\text{Area of poster sign} = \dfrac{1}{3} \times \dfrac{1}{9} = \dfrac{1}{27} \ \text{yard}^2\)
\(\text{Area of poster board} = 1 \ \text{yard}^2\)
Number of poster signs that can be cut :
\(\dfrac{\text{Area of poster board}}{\text{Area of poster sign}}\)
\(1 \ \text{yard}^2\div (\dfrac{1}{27} ) \ \text{yard}^2\)
\(1 \div \dfrac{1}{27}\)
\(1 \times \dfrac{27}{1}\)
\(\bold{= 27 \ poster \ signs}\)