Whats 4 1/3 x 3 1/5=? i need the answer please
Answers
Answer:
208/15
Step-by-step explanation:
4 1/3= 13/3
3 1/5= 16/5
208/15
Answer:
these answer would be 13/5 or 2 3/5

Related Questions
I’ll mark as BRANLIEST!!
Plz help me!!
(a^2-b) *division sign* 6; use a=5, and b=1
Answers
Answer:
4
Step-by-step explanation:
(a²-b)/ 6
=(5²-1)/ 6
=(25-1)/6
=24/6
=4
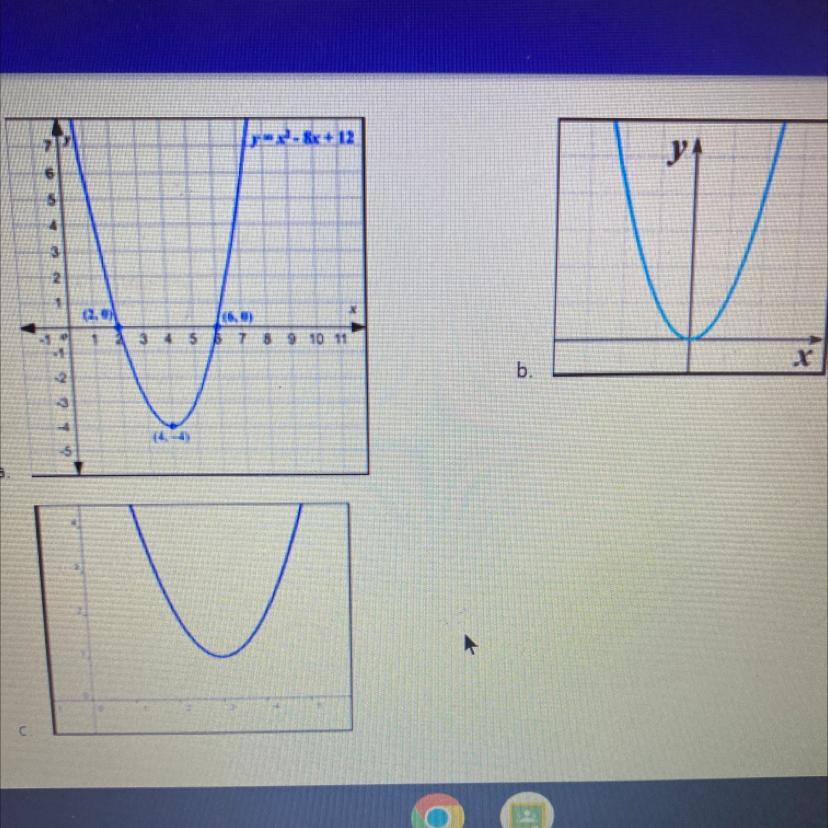
Is the discriminant positive, negative, or 0 for each graph below? Explain your choices in one or two sentences for each graph.
Answers
Step-by-step explanation:
Ok so as you may the quadratic formula is: \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
And the discriminant is: \(b^2-4ac\)
The reason this is so important, is because we can just calculate this and find how many solutions and what type of solutions a quadratic has.
Let's look at the three cases:
Positive:
If the discriminant is positive, there are two real solutions, since there will be a negative and positive square root solution, so there will be two distinct solutions
Negative:
If the discriminant is negative, there are two imaginary solutions, and what this really means is if you graph the equation, the quadratic never crosses the x-axis
Zero:
There is one real solution, since sqrt(0) doesn't have a "negative and positive solution", -0 = +0
So there is only one real solution
So in the top left graph, the discriminant is positive, since there are two distinct real solutions
The bottom left graph, the discriminant is negative, since the graph never crosses the x-axis, so the discriminant is negative, thus there are two imaginary solutions
The top right graph, the discriminant is zero, since there is only one real solution.
Answer:
a) positive
b) zero
c) negative
Step-by-step explanation:
Discriminant
\(b^2-4ac\quad\textsf{when}\:ax^2+bx+c=0\)
\(\textsf{when }\:b^2-4ac > 0 \implies \textsf{two real roots}\)
\(\textsf{when }\:b^2-4ac=0 \implies \textsf{one real root}\)
\(\textsf{when }\:b^2-4ac < 0 \implies \textsf{no real roots}\)
Graph a
The parabola intersects the x-axis twice. Therefore, there are two real roots and so the discriminant is positive.
Graph b
The parabola intersects the x-axis once. Therefore, there is one real root and so the discriminant is zero.
Graph c
The parabola does not intersect the x-axis. Therefore, there are no real roots and so the discriminant is negative.
Learn more about discriminants here:
https://brainly.com/question/27869538
https://brainly.com/question/27796651
a school takes feild triod tk the skating rink. when thd school brings 30 people they are charged 180 dollars. when the school brings 50 people they are charged 220 dollars. write and equation in slope intercept form to represent this situation and explain what the slope and y intercept represent.
Answers
Ramona works in a clothing store where she earns a base salary of $140 per day plus 14% of her daily sales. She sold $600 in clothing on Saturday and $1200 in clothing on Sunday. How much did she earn over the two days?
Answers
Answer: $ 532
Step-by-step explanation:
Given: Ramona works in a clothing store where she earns a base salary of $140 per day plus 14% of her daily sales.
She sold $600 in clothing on Saturday and $1200 in clothing on Sunday.
To find : Earning in two days.
Total sales she did in 2 days = $600+$1200 = $1800
Then, her total earning for 2 days = 2 x( Base salary)+ 14% of (Total sales)
= 2 x ($140) + (0.14) ($1800)
= $(280+252)
= $ 532
Hence, she earned $ 532 over the 2 days.
Answer:
$532
Step-by-step explanation:
Ramona worked for two days. So she would have already earned $280.
And she also earns 14% of $600 from the first day, and 14% of 1200.
14/100 * 600/1 = 8400/100 = $84
14/100 * 1200/1 = 16800/100 = $168
$280 + $84 + 168 = $532
Altogether, Ramona earned $532 in the total of two days! Wow that's more money then I get per month lol.
Hope this helps :D
- Anna
A fruit cup company delivers its fruit and two types of boxes, large and small a delivery of three large boxes and five small boxes is a total weight of 90 kg and delivery of nine boxes large and seven small boxes has a total weight of 216 kg how much does each type of box weigh
Answers
The weight of each large box is 18.5 kg and the weight of each small box is 7 kg.
Let's assume that the weight of each large box is x kg and the weight of each small box is y kg. There are two pieces of information to consider in this question, namely the number of boxes delivered and their total weight. The following two equations can be formed based on this information:
3x + 5y = 90 ......(1)9x + 7y = 216......
(2)Now we can solve this system of equations to find the values of x and y. We can use the elimination method to eliminate one variable from the equation. Multiplying equation (1) by 3 and equation (2) by 5, we get:
9x + 15y = 270......(3)45x + 35y = 1080.....
(4) Now, subtracting equation (3) from equation (4), we get:36x + 20y = 810.
Therefore, the weight of each large box is x = 18.5 kg, and the weight of each small box is y = 7 kg.
for such more questions on weight
https://brainly.com/question/29892643
#SPJ8
What is the linear equation of the line in point-slope form?

Answers
Answer:
4- 4Step-by-step explanation:
which is it ?
A : Not congruent
B : SAS
C : SSS
D : ASA

Answers
explanation, the triangles share a SIDE, the markings show a equal ANGLE, and the other markings show another equal SIDE. therefore they are congruent based on S(ide)A(ngle)S(ide)
64 = 4(p + 2) + 24 please solve step by step
Answers
Answer:
8
Step-by-step explanation:
Step-1 : Multiply the coefficient of the first term by the constant 1 • -16 = -16
Step-2 : Find two factors of -16 whose sum equals the coefficient of the middle term, which is 6 .
-16 + 1 = -15
-8 + 2 = -6
-4 + 4 = 0
-2 + 8 = 6 That's it
Step-3 : Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, -2 and 8
p2 - 2p + 8p - 16
Step-4 : Add up the first 2 terms, pulling out like factors :
p • (p-2)
Add up the last 2 terms, pulling out common factors :
8 • (p-2)
Step-5 : Add up the four terms of step 4 :
(p+8) • (p-2)
Which is the desired factorization
Answer:
p = 8
Step-by-step explanation:
64 = 4(p+2) + 24
64 = 4p + 8 + 24
64 = 4p + 32
32 = 4p
I substracted 32 from 64, and 32 deletes him self
8
I divided 32 by 4, and the 4p deletes himself
p = 8
Solve each for the missing variable
1. 9x + 15 = 96
Answers
Answer:
81
Step-by-step explanation:
my friend theres nothing on the world that will say that 96 - 15 = 9x
because 96-15= 81 and 81 + 15 equals 96
select three major processes that should be included in a model that explains the changes seen in the rock between figure 1 and figure 2
A. rainfall
B. Melting of ice
C. Plate Tectonics
D. Melting of Rock
E. Freezing of water
F. Deposition of sand
G. Crystallization of lava


Answers
Answer:
I think it's C and F. Don't depend on me tho I'm only in the 7th grade but I just told what I think is more logical
when entering units, capitalization is important. for example, m is the symbol for meter and m is the symbol for molarity. if the length of one side of a square is 12.0 m , what is the perimeter of the square?
Answers
The perimeter of the square is 40 meters.
The complete length that a square's edge in a plane covers is known as its perimeter. The route that encircles a form is called the perimeter.
By summing all the sides of a closed geometrical object (two-dimensional), the perimeter is determined. Since a square is a polygon with four equal sides, its perimeter will be equal to the sum of those sides.
Since all the sides of a square are equal, therefore, the perimeter of the square will be 4 times its side, i.e. 4 × Side. It is measured in units, such as m, cm, in, ft, etc.
Because a square has four sides of equal length, the perimeter is 12 m+12 m+12 m+12 m=48.0m
Thus, The perimeter of the square is 40 meters.
To know more about perimeter visit: brainly.com/question/6465134
#SPJ4
Each minute, a faucet allows 4/7 gallons of water to enter a large tub, and the drain allows 5/7 gallons to leave the tub.
What is the change in the amount of liquid in the tub after 1/4 minute?
Enter your answer as a fraction in lowest terms in the box.
gal.
Answers
Answer: -1/28 gallon
Step-by-step explanation:
divide both numbers by 4 since its 1/4 a minute (-5/7 ÷ 4 and 4/7 ÷ 4) then add them, (-5/28 + 4/28= -1/28)
Answer: -1/28 gallon
Step-by-step explanation:
Which graph is correct?

Answers
The graph of the inequality y ≥ (1/2)x - 1 and x - y > 1 is attached. Shannon's graph is correct.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables. Equations can either be linear, quadratic, cubic and so on depending on the degree.
Inequalities are used for the non equal comparison of numbers and variables.
Given the inequalities:
y ≥ (1/2)x - 1 (1)
and
x - y > 1 (2)
The graph of the inequality is attached. Shannon's graph is correct.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
What are they asking?

Answers
Please I need help ASAP what’s the distance between the 2 points

Answers
Answer:
7 grids
Step-by-step explanation:
-start at one of your points
-count up or down the y-axis to the other point.
-count along the x-axis to your other point.
-add the 2 lengths.
A population has a standard deviation of 39 . We take a random sample of size 30 from this population. Let Xbar be the sample mean and let Xtot be the sample sum of our sample. These are random variables. a) What is the variance of this population? b) What is the variance of Xtot? (to three decimal places) c) What is the standard deviation of Xtot? (to three decimal places) d) What is the variance of Xbar? (to three decimal places) e) What is the standard deviation of Xbar? (to three decimal places) f) What is the smallest sample size, n
r
which will make the standard deviation of Xtot at least 900 ? g) What is the smallest size sample, n, which will make the variance of Xtot at least 90000 ?
Answers
a) The variance of the population is equal to the square of the standard deviation. So, the variance of the population is (39)^2 = 1521.
b) The variance of Xtot is equal to the product of the variance of the population and the sample size. Since the sample size is 30, the variance of Xtot is 1521 * 30 = 45,630.
c) The standard deviation of Xtot is the square root of its variance. So, the standard deviation of Xtot is √(45,630) ≈ 213.869.
d) The variance of Xbar is equal to the variance of the population divided by the sample size. So, the variance of Xbar is 1521/30 ≈ 50.7.
e) The standard deviation of Xbar is the square root of its variance. So, the standard deviation of Xbar is √(50.7) ≈ 7.120.
f) To make the standard deviation of Xtot at least 900, we need to solve the following inequality:
45,630 ≥ 810,000
Since this inequality is not satisfied, there is no sample size that will make the standard deviation of Xtot at least 900.
g) To make the variance of Xtot at least 90,000, we need to solve the following inequality:
Variance of Xtot ≥ 90,000
45,630 ≥ 90,000
Since this inequality is not satisfied, there is no sample size that will make the variance of Xtot at least 90,000.
learn more about variance here:
https://brainly.com/question/31432390
#SPJ11
What is the slope of the linear relationship that contains the points (-3, 11/4) and (4,1)
Answers
Answer:
-3/28
Step-by-step explanation:
Slope = (change in y) / (change in x)
We can choose one of the points as our starting point, such as (-3, 11/4), and then calculate the change in y and change in x to get to the other point:
change in y = 1 - 11/4 = -3/4
change in x = 4 - (-3) = 7
Now we can substitute these values into the slope formula:
slope = (-3/4) / 7 = -3/28
Therefore, the slope of the linear relationship that contains the points (-3, 11/4) and (4,1) is -3/28.
Slope of the linear equation that contains the given points (-3,11/4) and (4,1) is -1/4.
A linear equation in 2 variables is of the form ax+by+c=0 where x and y are variables and a,b,c are constants.a and b respectively, are not equal to zero.
This form is called the general form of linear equation.
and the graph is a straight line.
the other form is slope intercept form which is given as: y=mx+c where m is the slope and c is the intercept.
another form is 2 point form of line which is given as :
y-y1= {(y2-y1)/(x2-x1)}(x-x1) here we put the values of the two known points in place of x1,y1, x2,y2.
for eg.y=2x +3 is a linear equation having m=2, c=3
y-2 =5(x-3) is a two point form linear equation.
and also there is one and only one line that passes through the two given points.If we are given two simultaneous linear equations then to find the common solution we either try to eliminate one variable by subtracting or replacing the value of that variable in terms of other variable.
for a single equation infinite points exist which satisfy the given equation.
for 2 equations we can check by knowing the ratios of a1/a2, b1/b2, c1/c2 respectively.
if a1/a2=b1/b2=c1/c2 then infinite solution exist.if a1/a2=b1/b2 but not c1/c2 then no solution existsif only b1/b2=c1/c2 then unique solution is found.now as given in the question let the given points be X(-3,11/4) and Y(4,1)
here x1= -3 ,y1=11/4 and X2=4, Y2=1
slope of the linear relationship is given by:
(y2-y1)/(x2-x1)
on putting values in above equation we get
(1-11/4)/(4-(-3))
=(-7/4)/7
=-1/4
Hence slope=-1/4
To know more about linear equations please visit:
https://brainly.com/question/28732353
6 trays with 72 muffins = muffins per tray
Answers
Answer:
12
Step-by-step explanation:
To find unit rate, you divide 72 by 6.
72/6=12.
So, there are 12 muffins per tray.
-hope it helps
measuring the entire population is usually preferred over measuring a sample from the population.
T/F
Answers
The given statement "Measuring the entire population is usually preferred over measuring a sample from the population" is False because measuring the entire population is often impractical or impossible.
When dealing with large populations, it is typically more feasible to gather data from a representative sample rather than measuring the entire population. This approach saves time, resources, and effort. Sampling allows statisticians to make reliable inferences about the population based on the characteristics observed in the sample.
Carefully chosen samples can accurately reflect the population's attributes and provide valuable insights.
However, it is crucial to ensure that the sample is representative and unbiased to avoid potential sampling errors and ensure the validity of the conclusions drawn from the data.
For more questions like Population click the link below:
https://brainly.com/question/27779235
#SPJ11
6. Jack is rolling down a hill. His plummet from the top of the hill to the bottom
can be expressed using the polynomial -3t2 + 13t. What is Jack's height after
3 seconds?
Answers
Answer:
Step-by-step explanation:
Tell him to not forget jill.
find the centroid of the region bounded by the given curves. y=12x,y=√x
Answers
The centroid of the region bounded by the curves y = 12x and y = √x is (72,1.88).
To find the centroid of the region bounded by the given curves y = 12x and y = √x, the following steps should be followed.
Step 1: Sketch the region bounded by the two curves to have an idea of what the region looks like.
Step 2: Determine the area of the region bounded by the two curves. The area A can be computed by evaluating the definite integral of the difference between the two functions. \(\[\int\limits_{0}^{144} (\sqrt{x}-12x)dx\]\) We solve for this integral below.\(\[\int\limits_{0}^{144} (\sqrt{x}-12x)dx = 64 - 1728 + \frac{2}{3}\sqrt{6}\] \[\int\limits_{0}^{144} (\sqrt{x}-12x)dx = -1663.30\]\)
Step 3: To find the centroid of the region, we need to determine the x and y coordinates of the centroid. The x-coordinate of the centroid is given by the formula below.
\(\[x = \frac{1}{A}\int\limits_{a}^{b} \frac{1}{2}(y_1^2-y_2^2)dx\]\)
where A is the area of the region, and y1 and y2 are the upper and lower functions, respectively. Substituting values, we obtain
\(\[x = \frac{1}{-1663.30}\int\limits_{0}^{144} \frac{1}{2}((\sqrt{x})^2-(12x)^2)dx\] \[x = 72\]\)
The y-coordinate of the centroid is given by the formula below.
\(\[y = \frac{1}{2A}\int\limits_{a}^{b}(y_1+y_2)\sqrt{(y_1-y_2)^2+4dx}\]\)
Substituting values, we obtain \(\[y = \frac{1}{2(-1663.30)}\int\limits_{0}^{144}(12x+\sqrt{x})\sqrt{(\sqrt{x}-12x)^2+4dx}\] \[y = 1.88\]\)
For more such questions on centroid
https://brainly.com/question/7644338
#SPJ11
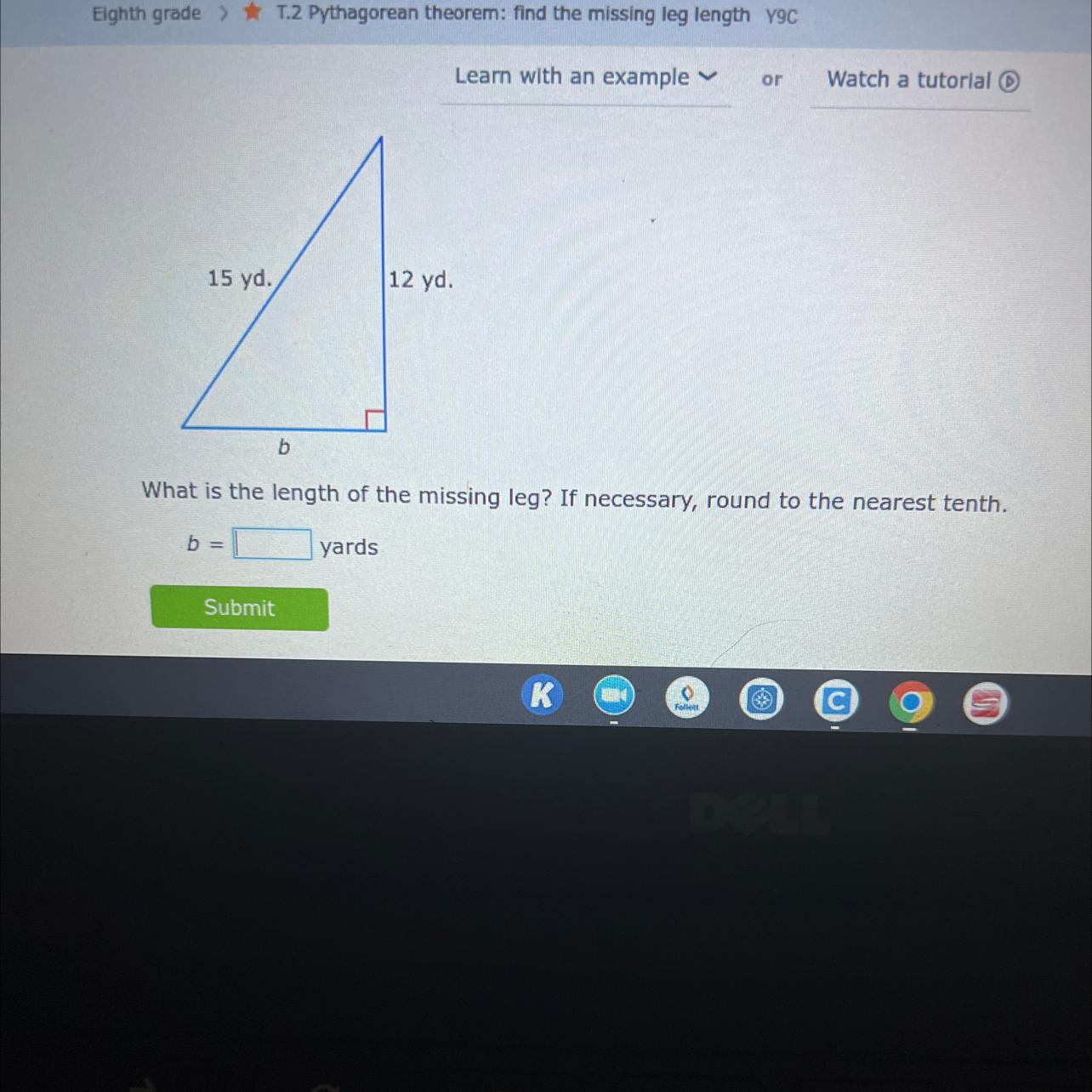
What is the length of the missing leg? If necessary, round to the nearest tenth.
Answers
Answer:
9 yards
Step-by-step explanation:
Length of missing leg = √ Hypotenuse² - Adjacent side²
b = \(\sqrt{15^{2} - 12^{2} } \\\sqrt{225 - 144} \\\sqrt{81} \\\)
b = 9 yd
Measurement Error on y i
( 1 point) Imagine the following model: y ∗
=Xβ+ε where X is n×k and β is k×1 (and k>2 ). Assume E[ε∣X]=0 and var[ε∣X]= σ ε
2
I n
. Unfortunately, you do not observe y ∗
. You observe y=y ∗
+η and estimate y=Xβ+ν by OLS. i) Write down the least squares problem for equation (3), obtain the first-order conditions, and isolate b (the resulting OLS estimator) (0.25 points). ii) Compute E(b) and describe in details the conditions under which b will be unbiased. Simply stating A3:E[ν∣X]=0 is not an acceptable answer (0.25 points). iii) Now, assuming that E[η∣X]=0 and var[η∣X]=σ η
2
I n
, compute var[b∣X] and explain how this variance will compare it to var[b ∗
∣X], where b ∗
is the OLS estimator for β in equation (1). That is, b ∗
is the OLS estimator that you would get if you could observe y ∗
and estimate equation (1)
Answers
The OLS estimator b in the presence of measurement error will be unbiased if certain conditions are met. The variance of b|X is larger than the variance of b*|X due to the additional measurement error.
i) The least squares problem for equation (3) is formulated as follows: minimize the sum of squared residuals, SSR(b) = (y - Xb)'(y - Xb). The first-order conditions give ∂SSR(b)/∂b = -2X'y + 2X'Xb = 0. Solving for b, we get b = (X'X)^(-1)X'y, which is the OLS estimator.
ii) The OLS estimator b will be unbiased if E(ν|X) = 0 and X is of full rank. Additionally, the error term ε should satisfy the classical linear model assumptions, including E(ε|X) = 0, var(ε|X) = σε^2In, and ε being uncorrelated with X.
iii) The variance of b|X is given by var(b|X) = σε^2(X'X)^(-1). Comparing it to var(b*|X), we find that var(b|X) is larger due to the presence of measurement error. The additional error term η introduces more variability into the estimated coefficients, leading to a larger variance compared to the scenario where y* is observed directly.
Therefore, The OLS estimator b in the presence of measurement error will be unbiased if certain conditions are met. The variance of b|X is larger than the variance of b*|X due to the additional measurement error.
To learn more about OLS click here
brainly.com/question/33206061
#SPJ11
find teh exact value of sin 2x given that sec x = 3/2 and csc y = 3 and x and y are in quadrant 1
Answers
The exact value of \(sin 2x\) is \(4√5/9.\)
Given that \(sec x = 3/2 and csc y = 3\)where x and y are in the 2x = 2 sin x quadrant, we need to find the exact value of sin 2x.
In the first quadrant, we have the following values of the trigonometric ratios:\(cos x = 2/3 and sin y = 3/5\)
Also, we know that sin \(2x = 2 sin x cos x.\)
Now, we need to find sin x.
Having sec x = 3/2, we can use the Pythagorean identity
\(^2x + 1 = sec^2xtan^2x + 1 = (3/2)^2tan^2x + 1 = 9/4tan^2x = 9/4 - 1 = 5/4tan x = ± √(5/4) = ± √5/2\)
As x is in the first quadrant, it lies between 0° and 90°.
Therefore, x cannot be negative.
Hence ,\(tan x = √5/2sin x = tan x cos x = √5/2 * 2/3 = √5/3\)
Now, we can find sin 2x by using the value of sin x and cos x derived above sin \(2x = 2 sin x cos xsin 2x = 2 (√5/3) (2/3)sin 2x = 4√5/9\)
Therefore, the exact value of sin 2x is 4√5/9.
To know more about trigonometric visit :
https://brainly.com/question/29156330
#SPJ11
what is the answer for
(6t − 6t to the power of 2) + 14(4t + 4)
Answers
Answer: = 50t+56
Step-by-step explanation: (6t-6t x 2) +14( 4t+4)
=6t-6t x 2 +14(4t+4)
=6t-12t+14(4t+4)
=6t-12t+56t+56
=50t+56
0.5 ft
0,4 ft
0.8 ft
Volume of prism =
V = 0.04 ft
O V = 0.064 it
O V = 0.08 it
5) Find the area of the base for the triangular prism.
Type here to search
Bi

Answers
Answer:
Huh I don’t understand this one but I got you
Step-by-step explanation:
2) A theater is designed so that the first row has 20 seats. Each additional row has 4 more seats than the previous row. How many seats will be in the 40th row?
Answers
Answer:
there will be 176 seats in the 40th row
In a plot of probability of finding the electron in the hydrogen ground state versus the distance from the nucleus, the maximum occurs
Answers
In a plot of the probability of finding the electron in the hydrogen ground state versus the distance from the nucleus, the maximum occurs (A) at a0. the first Bohr radius.
What is an electron?The electron is a subatomic particle with a negative one elementary charge electric charge. Electrons are the first generation of the lepton particle family and are widely regarded as elementary particles due to the lack of known components or substructure.Electron in the hydrogen:
Hydrogen has the simplest electron configuration to write because it just contains one electron. There is essentially only one electron surrounding the Hydrogen nucleus. Because hydrogen only has one electron, its configuration is 1s1.The maximum occurs at a0, the first Bohr radius, in a plot showing the chance of finding the electron in the hydrogen ground state vs the distance from the nucleus.Therefore, in a plot of the probability of finding the electron in the hydrogen ground state versus the distance from the nucleus, the maximum occurs (A) at a0. the first Bohr radius.
Know more about electrons here:
https://brainly.com/question/860094
#SPJ4
The complete question is given below:
In a plot of the probability of finding the electron in the hydrogen ground state versus the distance from the nucleus, the maximum occurs:
A. at a0. the first Bohr radius
B. at slightly less than a0
C. at slightly more than a0
D. at 2 a0
E. at a0/2
Evaluate the followinh integral as written In 9∫0 9∫ey 7y/x dx dy In 9∫0 9∫ey 7y/x dx dy=
Answers
Therefore, the value of the given double integral is approximately 1634.449.
The double integral:
∫ from y=0 to y=9 [ ∫ from x=In y to x=9 of \((7y/x) e^y dx ]\) dy
Using integration by parts, we can evaluate the inner integral as:
∫ from x=In y to x=9 of \((7y/x) e^y dx = [7y/e^x]\) evaluated from x=In y to x=9
= \(7y(e^{-9} - e^{(-lny)}) = 7y(1/y - 1/e^9) = 7 - 7e^{(9-y)\)
Substituting this back into the original double integral and evaluating the integral with respect to x, we get:
∫ from y=0 to y=9 \([ 7y - 7y e^{(9-y)} ] dy\)
Using integration by parts again, we can evaluate this integral as:
\([ 7y^2/2 + 7y e^{(9-y)} - 49 e^{(9-y) ]\) evaluated from y=0 to y=9
= \(3309/2 - 343 e^{-9\)
So, the value of the given double integral is approximately 1634.449.
Learn more about integral visit: brainly.com/question/30094386
#SPJ4
What is an equation of the line that passes through the points (6, 8) and (-3, 2)?
Answers
Answer:
y = 3/2x - 1
Step-by-step explanation:
2 - 8 / -3 -6 = -6 / -9 = 2/3
y - 8 = 3/2 (x - 6)
y - 8 = 3/2x - 9
y = 3/2x - 1