Which correctly explains the number of solutions of the following system of linear
equations?
- 3x + 3y = 12
y = x + 4
А The graphs of the equations are parallel lines because they have the same slope
but different y-intercepts. The system has no solution.
B The graphs of the equations are lines that intersect at one point because the
equations have the same slope but different y-intercepts. The system has
exactly one solution.
с
The graphs of the equations are lines that intersect at one point because the
equations have the same slope and same y-intercept. The system has exactly
one solution.
D The graphs of the equations are the same line because the equations have the
same slope and same y-intercept. The system has infinitely many solutions.
Answers
Answer:
D I dont know if im right though
Step-by-step explanation:
The system of equations are same and graphs of the equations are the same line because the equations have the same slope and same y-intercept. The system has infinitely many solutions.
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of line be represented as A
Now , the value of A is
The first equation is -3x + 3y = 12 be equation (1)
y = x + 4 be equation (2)
Adding 3x on both sides , we get
3y = 3x + 12
Divide by 3 on both sides , we get
y = x + 4 be equation (3)
So , the equation ( 2 ) is same as equation ( 3 )
Now , the slope of the equation is m = 1 and the y intercept is b = 4
Hence , the equations have infinite solutions
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ2
Related Questions
please help asap, it's for homework

Answers
Answer:
The slope is 10/1 so +10
Step-by-step explanation:
Hope this helps !!!
Answer:
10.
Step-by-step explanation:
Picking out 2 convenient points, (3, 30) and (0, 0):
Slope = (30-0)/(3-0)
= 30/3
= 10.
What is the volume of a sphere with a radius of 60.5 ft, rounded to the nearest tenth
of a cubic foot?
Answers
Answer:
If rounded to the nearest tenth of a cubic foot, would be: 927587.2
Step-by-step explanation:
The equation of finding the equation of the volume of a sphere is "4π\(\frac{radius^{3} }{3}\)"
If values are inserted in for radius as 60.5, the answer will be 927587.2 when rounded to the nearest tenths.
Hope this helps!
the set of all positive integers that are divisible by both 15 and 35 is infinite. what is the least positive integer in this set?550105210525
Answers
The least positive integer that will be divisible by both 15 and 35 will be 105.
The given integers are 15 and 35.
As we know that the least positive integer will be divisible by both 15 and 35 will be LCM ( least common factor) of 15 and 35.
The least common multiple of LCM of two integers is the common multiple of two numbers such that it is the least among all common multiples.
For example, LCM of 3 and 5 will be 15 because among all common multiples of 3 and 5, 15 will be least common multiple.
For LCM of 15 and 35, let's write multiples of both the numbers.
Multiples of 15 = 15,30,45,60,75,90,105,120,135,150,165,180,195,210,....
Multiples of 35= 35,70,105,140,175,210,...
We can see that 105 and 210 are two common multiples out of which 105 is the least multiple.
Therefore, the least positive integer that will be divisible by both 15 and 35 will be 105.
To know more about positive integer go throughthrough:-
https://brainly.com/question/31067729
#SPJ4
A company wants to evaluate the effects of a reduction in material cost of 3 percent and an increase in sales of 15 percent on a product with the following current characteristics: labor costs of $1,250,000, material costs of $5,000,000, overhead of $710,000, and sales of $8,000,000. What are the effects on net income with a 3 percent reduction in material costs? What is the effect with a 15 percent increase in sales?
Answers
The effect on net income with a 3 percent reduction in material costs is a decrease of $150,000. The effect on net income with a 15 percent increase in sales is an increase of $1,200,000.
To calculate the effects on net income, we need to consider the impact of the changes in material costs and sales on the company's financials.
First, let's calculate the effect of a 3 percent reduction in material costs. The current material costs are $5,000,000, so a 3 percent reduction would be 0.03 * $5,000,000 = $150,000. Since material costs are an expense, a reduction in material costs would lead to a decrease in expenses, which in turn would increase net income by the same amount.
Next, let's calculate the effect of a 15 percent increase in sales. The current sales are $8,000,000, so a 15 percent increase would be 0.15 * $8,000,000 = $1,200,000. An increase in sales would directly increase revenue, leading to an increase in net income.
Therefore, the effects on net income with a 3 percent reduction in material costs is a decrease of $150,000, and the effect with a 15 percent increase in sales is an increase of $1,200,000.
Learn more about sales here:
https://brainly.com/question/24951536
#SPJ11
Please help me this is due tomorrow

Answers
Answer:
Math test
Step-by-step explanation:
Math test:
(score/possible points) * 100 = %
(14/17)*100 = 82.35%
English Test:
(score/possible points) * 100 = %
(31/39)*100 = 79.48%
Therefor they did better on their math test
If 25 people start a race, in how many different ways can the top 2 finishers be determined?
Answers
There are total 600 number of ways or permutations the top two finishers can be determined.
According to the given question.
Total number of people who are participating in a race = 25
In 25 participants the total number of participants to be selected to finish the race = 2
As we know that "a permutation is a mathematical calculation of the number of ways a particular set can be arranged, where the order of the arrangement matters". Which can be calculated as
\(^{n}P_{r} = \frac{n!}{(n-r)!}\)
Where,
\(^{n} P_{r}\) is the number of permutations
n is the total number of objects
r is the numbers of objects to be selected
Thereofore,
The total number of ways, or permutaions the two top finishers can be determined is given by
\(^{25} P_{2}\)
= 25!/(25-2)!
= 25!/23!
= 25 × 24 × 23!/23!
= 25 × 24
= 600
Hence, there are total 600 ways or number of permutations the top two finishers can be determined.
Find out more information about permutations or number of ways here:
https://brainly.com/question/28021983
#SPJ4
4. What are the Z-scores for the following Confidence Interval levels? Remember, you MUST account for both tails of the curve, positive and negative, when identifying each. That means you will need to do a little math to obtain the correct z-value. 3 Points 68%= 85% = 99% =
Answers
In order to calculate the z-scores for the given Confidence Interval (CI) levels, we need to use the Z-table. It is also known as the standard normal distribution table. Here are the z-scores for the given Confidence Interval levels:1. 68% CI: The confidence interval corresponds to 1 standard deviation on each side of the mean.
Thus, the z-score for the 68% \(CI is ±1.00.2. 85% CI\): The confidence interval corresponds to 1.44 standard deviations on each side of the mean.
We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.85)/2)z = invNorm(0.925)z ≈ ±1.44\)Note that invNorm is the inverse normal cumulative distribution function (CDF) which tells us the z-score given a certain area under the curve.3. 99% CI: The confidence interval corresponds to 2.58 standard deviations on each side of the mean. We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.99)/2)z = invNorm(0.995)z ≈ ±2.58\)
Note that in general, to calculate the z-score for a CI level of (100 - α)% where α is the level of significance, we can use the following formula:\(z = invNorm((1 + α/100)/2)\) Hope this helps!
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
The sum of the numbers (112)3 and (211)3 is ( ____ )3 and their product is ( ____ )3.
Answers
(112)3 =336
(211)3 =633
sum of the numbers:
(112)3 +(211)3=
336+633=
969
product of the numbers:
(112)3 × (211)3=
336×633=
212688
Using the Law of Detachment if a polynomial is prime, then it cannot be factored. 5x+13y is prime.
Answers
Answer and Step-by-step explanation: Law of deduction is a mathematical logic that states the following:
1) If p happens, then q happens;
2) p is true;
Then, a there is a third statement that is
3) q is also true.
In this question,
If a polynomial is prime, then it cannot be factored.
Statement p is that 5x + 13y is a polynomial and is prime, i.e., p is true.
Statement q is that "it cannot be factored"
Therefore, 5x + 13y cannot be factored.
The law of detachment is used to confirm or refute a claim.
The true statement is: 5x + 13y cannot be factored
The law of detachment states that; for statements p and q
(1) If p then q
(2) p
If the above statements are true, then the following statement is true
(3) q
The statements in the question can be represented as:
(1) If 5x + 3y is a polynomial and is prime then it cannot be factored
(2) It cannot be factored
Using the above representations of p and q, as an illustration; the third statement would be:
(3) 5x + 3y is a polynomial and is prime
Since the third statement is true, then we can conclude that
5x + 13y cannot be factored
Read more about law of detachment at:
https://brainly.com/question/13966470
What is 8.7x3.9 in a step by step
Answers
X3.9
———
87 times 9 is 783 + 30 times 87 is 2610 so 3393 now since there are 2 decimal spots you put a decimal 2 over to make 33.93
A random sample of 1001 Americans aged 18-24 years showed that 51% believe their health is extremely important. The interval that is 95% certain to contain the proportion of all 18-24 year olds who believe that their health is extremely important is
Answers
Between 48% and 54% believe that their health is extremely important.
According to the statement
Given that a random sample of 1001 Americans aged 18-24 years showed that 51% believe their health is extremely important.
Here
Sample size n =1001
sample proportion p = 0.51
By these values we calculate the Standard error of proportion.
So, Standard error of proportion = 0.0158.
Since sample size is sufficiently large we can take Z critical value for confidence interval
Z critical value for 95% = 1.96
Margin of error = ±1.96*std error
= ±0.0310
confidence interval = 0.51 ±0.0310
= (0.48, 0.54)
So, Between 48% and 54% believe that their health is extremely important.
Learn more about PROPORTION here https://brainly.com/question/870035
#SPJ4
Which floating-point literal correctly represents the scientific notation value: 2.3 x 10^7?
Answers
The floating-point literal that correctly represents the scientific notation value: 2.3 x 10^7 will be A. 2.3e^7.
What is scientific notation?It should be noted that scientific notation simply means. way that's used to express numbers that are either too large or too small to be written in decimal form.
Therefore, it should be noted that the floating-point literal that correctly represents the scientific notation value: 2.3 x 10^7 will be:
= 2.3 × 20^7
= 2.3 × e^7
= 2.3e7
The correct option is A.
Learn more about scientific notation on:
brainly.com/question/106363
#SPJ1
Which floating-point literal correctly represents the scientific notation value: 2.3 x 10^7?
a. 2.3e^7
b. 2.3 × 10e^7
c. 2.3e × 10^7
d. 2.3 × e^7
How much will it cost to fill a
13-gallon gas tank at $2.30 per gallon?
Answers
Answer:
$29.90
Step-by-step explanation:
Just multiply gallons by price:
13 gallons x \(\frac{2.30 dollars}{1 gallon}\) = 29.9
Evaluate the following expression: \[ 1.723 \times 10^{2}+7.38 \times 10^{3} \] Type answer:
Answers
The sum of expression \(1.723 \times 10^{2}\) and \(7.38 \times 10^{3}\) is \(7.5523 \times 10^{3}\). The numbers in scientific notation are added by summing the coefficients while keeping the exponent unchanged.
In scientific notation, numbers are expressed as a coefficient multiplied by a power of 10. To add numbers in scientific notation, we need to ensure that the powers of 10 are the same.
In this case, both numbers are already in scientific notation with powers of 10. We can directly add the coefficients while keeping the exponent the same.
Adding \(1.723 \times 10^2\) and \(7.38 \times 10^3\) gives us a sum of \(7.5523 \times 10^3\). The coefficient represents the numerical value, and the power of 10 indicates the magnitude.
Thus, the expression \(1.723 \times 10^2 + 7.38 \times 10^3\) evaluates to \(7.5523 \times 10^3\), indicating a significant increase in magnitude compared to the individual numbers.
Learn more about Expression click here :brainly.com/question/24734894
#SPJ11
What is the quotient? x 5 )4x2 14x − 9 4x 6 4x 6 − 4x − 6 4x − 6 −
Answers
The quotient of dividing the expression 4x² + 14x - 9 by 4x - 6 is x + 5.
The quotient is the result of dividing one number by another. In this case, we are dividing the expression 4x² + 14x - 9 by 4x - 6.
To find the quotient, we can use polynomial long division.
1. Start by dividing the first term of the numerator (4x²) by the first term of the denominator (4x). The result is x.
2. Multiply the entire denominator (4x - 6) by the quotient we just found (x). This gives us 4x² - 6x.
3. Subtract the result obtained in step 2 from the numerator (4x² + 14x - 9). This gives us (4x² + 14x - 9) - (4x² - 6x) = 20x - 9.
4. Bring down the next term from the numerator, which is 20x.
5. Divide the first term of the new expression (20x) by the first term of the denominator (4x). The result is 5.
6. Multiply the entire denominator (4x - 6) by the quotient we just found (5). This gives us 20x - 30.
7. Subtract the result obtained in step 6 from the expression obtained in step 5 (20x - 30) from (20x - 9). This gives us (-30 + 9) = -21.
8. Since there are no more terms left in the numerator, the division process is complete.
Therefore, the quotient is x + 5.
To know more about polynomial long division, refer to the link below:
https://brainly.com/question/32856619#
#SPJ11
I know I’m dumb
But please I need a answer!

Answers
Answer:
A. 771
Hope this helps
answer quickly !!! Pls

Answers
Answer:
(6 × 5) + (6 × 3) = 6 × (5 + 3)
Step-by-step explanation:
Since both 5 and 3 are being multiplied by 6, the total would be 6 multiplied by the sum of 5 and 3.
find mFE arc measure
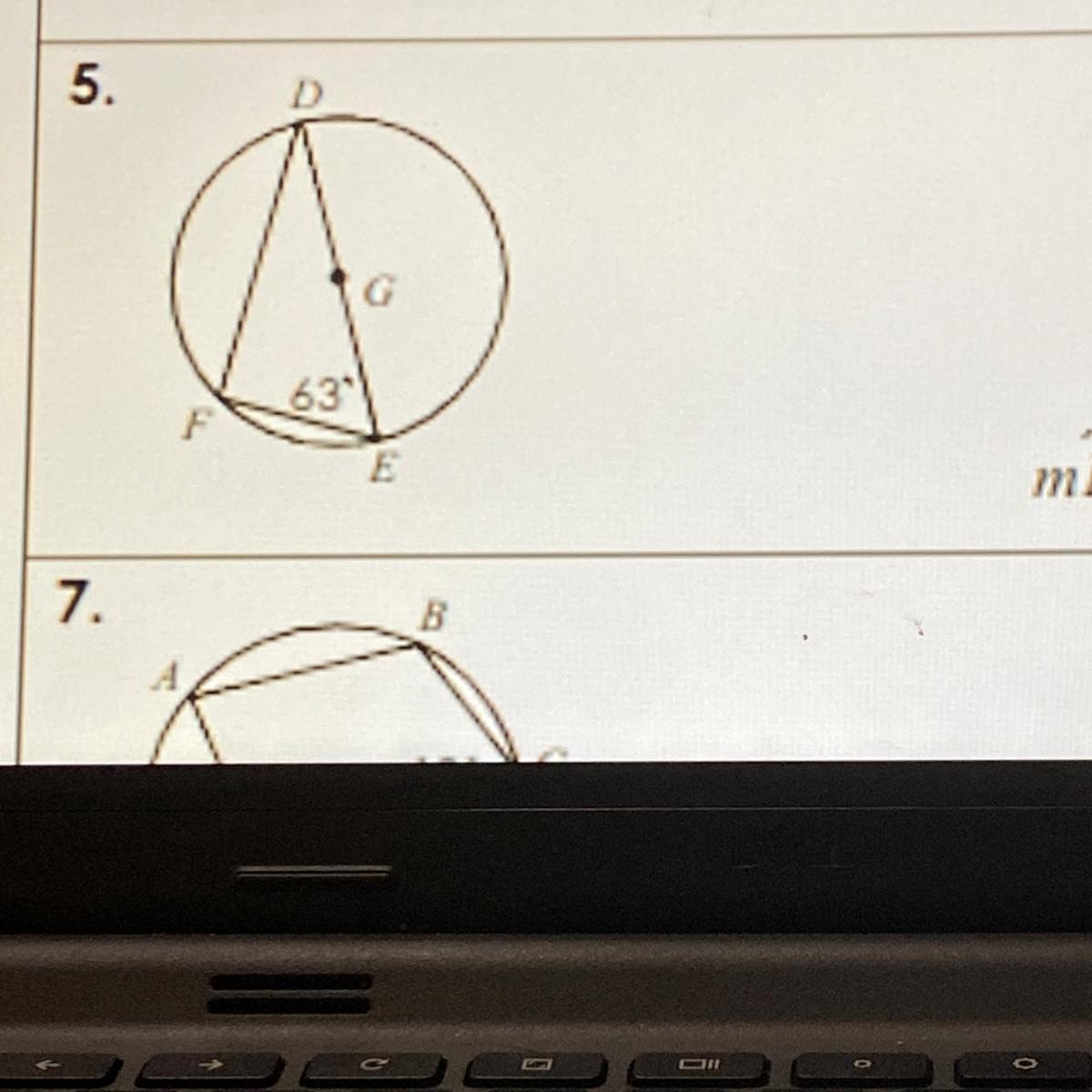
Answers
Question 5
FD = 63 • 2 or 126°. The reason for this is the fact that 63° is an inscribed angle.
DE is a straight line. A straight line measures 180°.
The measure of a circle is 360°.
FE = 360° - 180° - 126°
FE = 54°.
Remember: FE is a minor arc.
Understand?
Done!
Which angle is formed by EA−→
and EG−→−?
Select all that apply.

Answers
Answer:
Step-by-step explanation:
\(\angle 2,\angle AEG, \angle GEB\)
Graph Y equals |x|-5

Answers
Answer:
graph C
Step-by-step explanation:
when X= 0
Y ---> -5
so , answer is graph C
Answer:
c
Step-by-step explanation:
the graph of | x | has its vertex at the origin and has shape V
the graph of | x | - 5 is the graph of | x | translated 5 units vertically down.
That is graph c represents | x | - 5
nele is raising a baby squirrel. she weighs the squirrel each day and makes a note of the weight. after one month, she decides that she wants to create a display to show the squirrel's weights each day over the last month. which type of graph best represents the data?
Answers
Each day's weight can then be plotted as a point on the graph, and a line can be drawn connecting the points to show the trend in the squirrel's weight over time.
What is Graph ?
Graph can be defined as visual representation of data using given ordered pairs.
For tracking the weight of a baby squirrel over a month, a line graph would be the best option.
A line graph is used to display data that changes continuously over time, making it ideal for showing the daily weight of the squirrel over the course of a month.
The horizontal axis can represent the time (in days), and the vertical axis can represent the weight of the squirrel.
Therefore, Each day's weight can then be plotted as a point on the graph, and a line can be drawn connecting the points to show the trend in the squirrel's weight over time.
To learn more about Graph from given link.
https://brainly.com/question/17267403
#SPJ1
Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.]
f(x) = x⁴ - 6x² + 1, a = 2
Answers
This is the Taylor series expansion for the function f(x) = x⁴ - 6x² + 1 centered at a = 2.
What is Taylor Series?
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the derivative of the function at a single point. For most common functions, the function and the sum of its Taylor series near this point are the same.
To find the Taylor series for the function f(x) = x⁴ - 6x² + 1 centered at a = 2, we can use the formula for the Taylor series expansion:
f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)²/2! + f'''(a)(x - a)³/3! + ...
First, let's find the values of f(a) and its derivatives at x = a = 2:
f(2) = (2)⁴ - 6(2)² + 1 = 16 - 24 + 1 = -7
f'(x) = 4x³ - 12x
f'(2) = 4(2)³ - 12(2) = 32 - 24 = 8
f''(x) = 12x² - 12
f''(2) = 12(2)² - 12 = 48 - 12 = 36
f'''(x) = 24x
f'''(2) = 24(2) = 48
Now, we can substitute these values into the Taylor series formula:
f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)²/2! + f'''(a)(x - a)³/3! + ...
f(x) = -7 + 8(x - 2)/1! + 36(x - 2)²/2! + 48(x - 2)³/3! + ...
Simplifying the terms:
f(x) = -7 + 8(x - 2) + 18(x - 2)² + 8(x - 2)³ + ...
This is the Taylor series expansion for the function f(x) = x⁴ - 6x² + 1 centered at a = 2.
To learn more about Taylor Series from the given link
https://brainly.com/question/12800011
#SPJ4
At a pet store, 67% of customers get a leash for their dog. Only 32% of customers get a leash for their dog and get their dog a treat. What is the probability that a customer who gets a leash for their dog also gets their dog a treat?
Answers
Answer:
The probability of a customer getting a leash for their dog along with a treat for their doctors is 1/2.09
Step-by-step explanation:
This is example of conditional probability.
Let A represents the % of customer getting a leash for their dogs
Let B represents the % customer getting a leash + treat for their dogs
As we know-
P(A|B)=P(A and B)/P(B)
So the probability is
P(A|B)= 0.32/0.67 = 1/2.09
You and a companion are driving a twisty stretch of road in a car with a speedometer but no odometer. To find out how long this road is, you record the car's velocity at 10-second intervals Time (s) 0 10 20 30 40 50 60 Velocity (ft/s) 0 33 10 25 17 29 11 Time (s) 70 80 90 100 110 120 Velocity (ft/s) 34 36 15 41 20 24 a. Estimate the length of the road using left-endpoint values ft
Answers
The estimated length of the road using left-endpoint values is approximately 1510 feet.
To estimate the length of the road using left-endpoint values, we will use the velocity data provided and apply the Left Riemann Sum method. This method involves multiplying the velocity value at each time interval's left endpoint by the interval length (10 seconds) and summing the products.
Here are the steps:
1. Identify the left-endpoint values of the velocity at each time interval:
0 ft/s, 33 ft/s, 10 ft/s, 25 ft/s, 17 ft/s, 29 ft/s, 11 ft/s, 34 ft/s, 36 ft/s, 15 ft/s, 41 ft/s, and 20 ft/s.
2. Multiply each left-endpoint value by the interval length (10 seconds):
0 * 10 = 0
33 * 10 = 330
10 * 10 = 100
25 * 10 = 250
17 * 10 = 170
29 * 10 = 290
11 * 10 = 110
34 * 10 = 340
36 * 10 = 360
15 * 10 = 150
41 * 10 = 410
20 * 10 = 200
3. Sum the products to get the estimated length of the road:
0 + 330 + 100 + 250 + 170 + 290 + 110 + 340 + 360 + 150 + 410 + 200 = 1510 ft
So, the estimated length of the road using left-endpoint values is approximately 1510 feet.
To know more about Riemann Sum method visit:
brainly.com/question/24138395
#SPJ11
Question 1 of 14
Sofia's family members are choosing numbers to see in
what order they will choose gifts. They will spin a spinner
with eight sections. The sections are numbered 1 through
8, and all sections are the same size.
What is the probability of spinning a number greater than 3?
A.
8
5
B.
3
8
8
Answers
Answer:
c
Step-by-step explanation:
count
Answer:
C
Step-by-step explanation:
Paul, Linda, and Aaron make handmade cards. Paul can make 1 card for every 3 cards Linda makes. Linda can make 3 cards for every 2 cards that Aaron makes. During a week, Aaron makes 72 cards.
How many more cards does Linda make than Paul during the week?
Answers
Answer:
Linda makes 3 more cards than Paul.
Step-by-step explanation:
Let's express the affirmations into equations:
Paul (P) can make 1 card for every 3 cards Linda (L) makes:
\( \frac{P}{L} = \frac{1}{3} \)
\( 3P = 1L \) (1)
Linda can make 3 cards for every 2 cards that Aaron (A) makes:
\( \frac{L}{A} = \frac{3}{2} \)
\( 2L = 3A \) (2)
During a week, Aaron makes 72 cards, hence the number of cards of Linda and Paul can be calculated as follows:
From equation (2):
\( L = \frac{3}{2}A = \frac{3}{2}72 = 108 \)
Now, from equation (1):
\( P = \frac{1}{3}L = \frac{1}{3}108 = 36 \)
Finally, the number of cards that Linda makes more than Paul is:
\( \frac{L}{P} = \frac{108}{36} = 3 \)
Therefore, Linda makes 3 more cards than Paul.
I hope it helps you!
Number of more cards Linda made than Paul for the week is; she made 72 more cards than Paul for the week.
We are told that;
Paul can make 1 card for every 3 cards Linda makes. Let number of card Paul makes be p and let number of cards Linda makes be L. Thus, we have;
p/l = 1/3
Thus;
l = 3p
Linda can make 3 cards for every 2 cards that Aaron makes. If number of cards that Aaron makes is a, then;
l/a = 3/2
l = 3a/2
Now, we are told that Aaron made 72 cards in a week. Thus, a = 72 and so we have;
l = (3 × 72)/2
l = 108 cards for the week
Since l = 3p, then;
p = l/3
p = 108/3
p = 36 cards for the week.
Thus;
Difference between number of Linda's cards and Paul's cards = 108 - 36 = 72
Thus,linda made 72 more cards than Paul for the week.
Read more at; https://brainly.com/question/16725328
4+(−634) please answer
Answers
The solution to the expression 4+(−634) is -630
How to evaluate the expression?From the question, we have the following parameters that can be used in our computation:
4+(−634)
Rewrite the expression properly
So, we have the following representation
4 + (−634)
Remove the bracket in the above expression
This gives
4 + (−634) = 4 - 634
Evaluate the difference
4 + (−634) = -630
Hence, the solution is -630
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
How many paths are there from $A$ to $B,$ if you travel along the edges? You can travel along each edge at most once, but you can pass through the same point more than once. (You can pass through $B,$ as long as you end up at the point $B.$) [asy] unitsize(1.5 cm); draw((0,0)--dir(60)--(1,0)); draw((0,0)--(1,0)); draw((0,0)--dir(-60)--(1,0)); label("$A$", (0,0), W); label("$B$", (1,0), E); [/asy]
Answers
Answer:
There are $\boxed{3}$ paths from $A$ to $B.$
Write an example from daily life that uses each type of real number.
rational numbers
Answers
Write an example from daily life that uses rational numbers .
Real numbers that may be expressed as p/q, where p, q are integers, and q 0, are rational numbers. The money we have is a rational number. If we spend some sum out of it, it is subtraction of rational number.The running race involves rational numbers if you're an athlete.Rational numbers include the following:the distance runthe time needed to complete the distance,the number of competitors placing first, second, or thirdthe number of heartbeats you take per minute.We use fractions to represent taxes.If you split a pizza or any other food.When you finish a piece of your work, you indicate that you have done half, or 50%.Loan and mortgage interest rates.Savings account interest.To learn more about rational numbers, refer:
https://brainly.com/question/12088221
#SPJ4
8. Points P, Q, whose abscissae are 2 and 2+h, are taken on the curve y = 2x^2+1. Find the gradient of the chord PQ. To what value does this gradient approach as h decreases towards the value zero?
Answers
The gradient of the chord PQ is 2h + 8
What is the gradient of the chord?Let's first find the coordinates of points P and Q on the curve y = 2x^2+1.
Point P has an abscissa of 2, so its coordinates are (2, 2(2)^2+1) = (2, 9).
Point Q has an abscissa of 2+h, so its coordinates are (2+h, 2(2+h)^2+1) = (2+h, 2(4+4h+h^2)+1) = (2+h, 8+8h+2h^2+1) = (2+h, 2h^2+8h+9).
The gradient of the chord PQ is given by:
(m) = Δy /Δx
(m) = (2h^2+8h+9 - 9) / (2+h - 2)
(m) = (2h^2+8h) / (h)
(m) = 2h + 8
As h approaches zero, the gradient of the chord PQ approaches 8, because the term 2h becomes negligible compared to 8 when h is small. Therefore, the gradient of the tangent to the curve at point P is 8.
Learn more on gradient of a curve here;
https://brainly.com/question/29867655
#SPJ1