Write the word sentence as an equation.
The quotient of 36 and a number g is 9.
Answers
Answer:
\(\frac{36}{g}\)=9
Related Questions
MATH QUESTION ON SLOPESSSSSSS
Given: m = 3/2 and b = -1
The slope and y-intercept for a linear equation are given. Which graph matches this information?
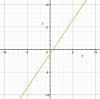


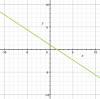
Answers
if the bathtub holds a total of 46.2 gallons , how many minutes would it take to fill
the entire tub ?
Answers
Step-by-step explanation:
It takes 3 minutes, at 17 gallons per minute, for the tap to fill the tub, so 51 gallons of water flow into the tub.
The capacity of the tub is 46.5 gallons; so in 3 minutes 51-46.5 = 4.5 gallons have leaked. That's a rate of 4.5/3 = 1.5 gallons per minute.
The amount of time it will take the tub to drain at that rate is 46.5/1.5 = 31 minutes.
Answer:
It takes 3 minutes, at 17 gallons per minute, for the tap to fill the tub, so 51 gallons of water flow into the tub.
Step-by-step explanation:
Name the algebraic property.
m2 ABC = m2 DEF
and
m2 DEF = m2 ABC
Answers
I hope I am right
Calculate the area of trapezium CDEF.

Answers
Answer:
i think 24 cm² is answer good luck

A carpenter has 2 pipes which are 60 dm and 72 dm long respectively. he cuts them into equal lengths. what is the greatest possible length of each pipe?
Answers
Using greatest common factor (GCF), the greatest possible length of each pipe is 12 dm.
The greatest common factor (GCF) of a set of numbers is defined as the largest common positive integer that divides each number into equal parts with zero remainder.
If a carpenter has 2 pipes which are 60 dm and 72 dm long, respectively and he cuts them into equal lengths, then the greatest possible length of each pipe is the GCF of 60 and 72.
60 : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
72 : 1, 2, 3, 4, 6, 8, 9, 12, 16, 24, 36, 72
common factors : 1, 2, 3, 4, 6, 12
GCF = 12
Hence, he should cut the two pipes into 12 dm long.
Learn more about greatest common factor (GCF) here: brainly.com/question/219464
#SPJ4
HELP ITS DUE IN 20 MIN

Answers
Answer:
48.5 cm (C).
Step-by-step explanation:
First, the area of the rectangle:
Length × width = 8 × 4 = 32cm²
Second, the area of the square:
Length × Length = 3 × 3 = 9cm²
Third area of the triangle:
To find the height:
8 - 3 = 5 cm
Base:
3 cm
½ × base × height = ½ × 3 × 5 = 15/2 = 7.5cm²
Now add all of them together:
32 + 9 + 7.5 = 48.5 cm²
48.5 cm² is the answer.
What is the confidence level for the interval x ± 1.43????⁄ n ? (Round your answer to one decimal place.)
_________ %
Answers
The confidence level for the interval x ± 1.43/√n is 84.7%.
How to find the confidence level?
The confidence level for the interval x ± 1.43/√n can be found by identifying the critical value and looking it up in a standard normal (z) table.Identify the critical value: In this case, the critical value (z-score) is 1.43.
Look up the critical value in a standard normal (z) table: When you look up 1.43 in a z-table, you find the probability of 0.9236. This means that there is a 92.36% chance that a randomly selected value from the standard normal distribution lies within 1.43 standard deviations from the mean Calculate the confidence level: Since the interval is symmetric, we need to consider the area in both tails of the distribution. To do this, we double the area we found in step 2 (0.9236) and subtract it from 1.
Confidence level = (1 - 2*(1-0.9236)) * 100 = (1 - 2*0.0764) * 100 = (1 - 0.1528) * 100 = 84.72%
Round your answer to one decimal place: 84.7%.
So, the confidence level for the interval x ± 1.43/√n is 84.7%.
Learn more about confidence level
brainly.com/question/30229866
#SPJ11
The confidence level for the interval x ± 1.43/√n can be calculated based on the sample size and the desired level of confidence.
How can we calculate the confidence level?The confidence level for a confidence interval is expressed as a percentage and represents the probability that the true population parameter falls within the interval. The confidence level is typically chosen by the researcher and is often set to 90%, 95%, or 99%.
To calculate the confidence interval for a given sample, you would need to know the sample size, the sample mean, and the sample standard deviation. Then, you could use a formula to calculate the interval, such as:
x ± z * (s / √n)
where x is the sample mean, s is the sample standard deviation, n is the sample size, and z is the z-score for the desired level of confidence.
Once you have calculated the interval, you can state the confidence level as the probability that the true population parameter falls within the interval.
Learn more about confidence intervals
brainly.com/question/24131141
#SPJ11
Solve for x. Make sure to show all your work. 21=3(x+6)
Answers
Answer:
1 is correct answer
Step-by-step explanation:
\(21 = 3(x + 6) \\ 21 = 3x + 18 \\ 21 - 18 = 3x \\ 3 = 3x \\ x = \frac{3}{3} \\ x = 1\)
hope it helped you:)
Mack thinks that natural numbers are a subset of irrational numbers. Is Mack correct?
Answers
Answer:
He is incorrect.Because if they are irrational they are the opposite.
Step-by-step explanation:
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a , b , c in each case :
i ) -2x + 3y = 6
ii) 2x = -5y
Answers
\( {\qquad\qquad\huge\underline{{\sf Answer}}} \)
Let's solve ~
Question - 1 :
\(\qquad \sf \dashrightarrow \: - 2x + 3y = 6\)
\(\qquad \sf \dashrightarrow \: - 2x + 3y - 6\)
\(\qquad \sf \dashrightarrow \: (- 2)x + (3)y + (- 6)\)
comparing it to general equation, we get :
\( \sf\dashrightarrow \: a = - 2\)\( \sf\dashrightarrow \: b = 3\)\( \sf\dashrightarrow \: c= - 6\)Similarly,
Question - 2 :
\(\qquad \sf \dashrightarrow \: 2x = - 5y\)
\(\qquad \sf \dashrightarrow \: 2x + 5y = 0\)
\(\qquad \sf \dashrightarrow \: (2)x + (5)y + 0 = 0\)
comparing it with general equation, we get :
\( \sf\dashrightarrow \: a = 2\)\( \sf\dashrightarrow \: b = 5\)\( \sf\dashrightarrow \: c = 0\)The graph of the function f(x)= -3x+3 is shown.
What is the value of f(3)
What is the value of f(0)
What is the value of f(1)
May someone plz help meeeeeeeeeeee

Answers
Step-by-step explanation:
f(x)=-3x+3
f(3)=-9+3=-6
f(0)=0+3=3
f(1)=-3+3=0
the3 0 1 should be used in place of x and f(x) should be founs
Answer:
The functions are defined as:
f(3) = -6f(0) = 3f(1) = 0Step-by-step explanation:
We are given a function:
\(\bullet \ \ \ f(x) = -3x + 3\)
We need to find the values of the function at:
f(3)f(0)f(1)When we replace the x in f(x) with a number, we are saying that "f of 3" or "f of 0" or "f of 1." This means that when we change the x in f(x), we need to also change the rest of the x-variables in the function.
Therefore, to solve f(3), every x must be changed to 3.
\(f(x) = -3x + 3\\\\f(3) = -3(3) + 3\\\\f(3) = -9 + 3\\\\f(3) = -6\)
We can follow the same method for f(0) and f(1).
\(f(x) = -3x + 3\\\\f(0) = -3(0) + 3\\\\f(0) = 0 + 3\\\\f(0) = 3\)
And finally, we can solve for f(1).
\(f(x) = -3x + 3\\\\f(1) = -3(1) + 3\\\\f(1) = -3 + 3\\\\f(1) = 0\)
Therefore, the function is defined at each value as:
f(3) = -6f(0) = 3f(1) = 0An airplane travels 4,000miles in 8 hours. What is the speed?
Answers
Answer:500 mile per hour
Step-by-step explanation: 4000/8=500
Answer: 500mi/h
Step-by-step explanation: Speed = distance/time.
distance = 4000mi(miles)
Time =8h(hours)
4000mi/8h = 500mi/h
3/16 x 6 in the simplest form

Answers
The fraction 9/8 is the simplest form of the given fraction.
What is the fraction?A fraction is defined as a numerical representation of a part of a whole that represents a rational number.
The fraction is given in the question, as follows:
3/16 x 6
We have to determine the evaluation of the given fraction
As per the question, we have
3/16 x 6
Apply the multiplication operation,
18/16
Reduce the above fraction into the simplest form, and we get
9/8
Thus, the fraction 9/8 is the simplest form of the given fraction.
Learn more about the fraction here:
brainly.com/question/10354322
#SPJ2
you can use universal generalization (ug) to obtain a universal statement by generalizing only from a free variable, and not from a constant. true or false
Answers
True, you can use universal generalization (UG) to obtain a universal statement by generalizing only from a free variable, and not from a constant. Generalization involves making a statement that applies to all instances of the variable, while constants remain fixed and do not change in value.
True. Universal generalization (UG) allows us to derive a universal statement by generalizing from a free variable. General sampling deals with the fact that if something is true for everything, it must also be true for every specific thing called the constant c. Existential generalization deals with the fact that the special case c is true for at least one thing if it is true.
A free variable is a variable that is not bound by a quantifier, meaning it is not restricted to a specific value or range of values. In contrast, a constant is a variable that is already assigned a specific value and cannot be generalized over. Therefore, UG can only be applied to free variables and not constants.
Learn more about Variable:
brainly.com/question/29583350
#SPJ11
unless posted otherwise, what is the speed limit when passing a school building or school grounds when children are present?
Answers
unless posted otherwise, the speed limit when passing a school building or school grounds when children are present will be 25 mph.
A typical school zone speed limit in many US states is between 15 mph and 25 mph (25 and 40 km/h) except if generally posted. Oftentimes, school zone signs have the "When kids are available" notice.
This is illuminated in California's vehicle code section 22352(2), which expresses that the 25 mph limit "will likewise apply while drawing nearer or passing any school grounds which are not separated from the thruway by a wall, entryway, or one more actual hindrance while the grounds are being used by kids and the expressway is posted with a norm "SCHOOL" cautioning sign."
The law likewise applies to streets close to senior focuses with a posted "senior" cautioning sign.
to know more about speed click here:
https://brainly.com/question/13943409
#SPJ4
HELP PLEASE 15 [POINTS]
![HELP PLEASE 15 [POINTS]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/dIdJOX6v8pIT2ndyTuKtqj3sxL7evvfX.png)
Answers
Answer:
A
Step-by-step explanation:
I just used Pythagorean Theorem for this one
I hope this helps!!
Bob drew a line he thought was close to many of the points and found the equation of the line. He used the points (165, 168) and (174, 178) on his line to find the equation. What is the equation of Bob’s line? If entering decimal values, round to the tenths place.
What does Bob’s equation predict for the height of a person with an arm span of 162 cm? If entering a decimal value, round to the tenths place
Answers
We will see that the linear equation is:
y = 1.1*x -13.5
b) The predicted height is 164.7cm
How to get the linear equation?
A general linear equation is:
y = a*x + b
Where a is the slope and b is the y-intercept.
If we know that the line passes through (x₁, y₁) and (x₂, y₂), then we can write the slope as:
a = (y₂ - y₁)/(x₂ - x₁)
In this case, the line passes through (165, 168) and (174, 178), then the slope is:
a = (178 - 168)/(174 - 165) = 10/9 = 1.1
Then the line is:
y = 1.1*x + b
To get the value of b, we use one of the given points, for example if we use the first one (165, 168) we must have x = 165 and y = 168, replacing that we get:
168 = 1.1*165 + b
168 - 1.1*165 = b = -13.5
The equation is:
y = 1.1*x -13.5
Now we want to find the height of a person with an arm span of 162cm, then we replace x by 162 to get:
y = 1.1*162 -13.5 = 164.7
The predicted height is 164.7cm
If you want to learn more about linear equations, you can read:
https://brainly.com/question/1884491
What is the area of `∆STR`?
A.
30 square feet
B.
34.5 square feet
C.
57.5 square feet
D.
60 square feet
Answers
Answer:
its 30 a
Step-by-step explanation:
Answer:
Hello Ma'am Or Sir! The Correct Answer Is 30 Square feet.Step-by-step explanation:
Explanation:
A = (6 x 10)/2 = 60/2 = 30
Hope this helps!Which expression is equivalent to (4 x cubed) (2 x) superscript negative 4?
Answers
Answer:
section covers somplifying algebraic expressions
Step-by-step explanation:
(4\(x^{3}\))(2\(x^{-4}\)) = \(\frac{4x^{3} }{2x^{4} }\) = 2/x⇒Answer:
A) 1/4x
Step-by-step explanation:
Cause I took the test and got it right
how many different 7 card hands can be chosen from a standard 52 card deck
Answers
Using the combination formula, we calculate that there are 133,784,560 different 7-card hands that can be chosen from a standard 52-card deck.
A standard 52-card deck has 52 unique cards, and to find the number of different 7-card hands that can be chosen, we use the combination formula, which is C(52,7). This formula represents the number of ways to choose 7 cards out of a total of 52 cards, where order does not matter.
The formula for C(52,7) is derived by using factorials. For example, 52! represents 52 x 51 x 50 x 49 x 48 x 47 x 46 x ... x 2 x 1, which is the total number of ways to arrange all 52 cards. The denominator, 7! x 45!, represents the number of ways to arrange the 7 chosen cards out of 52, and also the number of ways to arrange the remaining 45 cards that were not chosen.
To know more about combination,
https://brainly.com/question/13877117
#SPJ11
Please help the question is in the picture that I attached

Answers
Answer:
-22
Step-by-step explanation:
f(-2) = -2(-2)^2 + 7(-2)
= -2(4) + 7(-2)
= -8 + -14
= -22
Answer: Children are dying in Palestine and you're more concerned about this? Shame what this world has come to. Explanation:
Step-by-step explanation:
Maya has a coin collection. She keeps 6 of the coins in her box, which is 2% of the collection. How many total coins are in her collection?
Answers
Answer:
300 coins
Step-by-step explanation:
The figure is transformed as shown in the diagram. Describe the transformation.
A) reflection, then rotation
B) rotation, then reflection
C) reflection, then dilation
D) translation, then dilation

Answers
Answer:
B) Rotation, then Reflection
for the integer data set containing 11, 13, 15, 17, x, and y, the unique mode, median, and mean form an increasing arithmetic sequence, in that order. what is the greatest possible value of y?
Answers
Given the integer data set containing 11, 13, 15, 17, x, and y, we know that the mode, median, and mean form an increasing arithmetic sequence.
Since the mode is the unique number that appears most frequently, either x or y must be equal to one of the existing numbers (11, 13, 15, or 17). Let's assume x is the mode. For the sequence to be increasing, the mode must be the smallest, so x = 11.
The median of the data set is the average of the two middle numbers when they are arranged in ascending order. With x = 11, the sorted sequence will be 11, 11, 13, 15, 17, and y. The median will be the average of 11 and 13, which is 12.
For the mean, we have (11+11+13+15+17+y)/6. We know the mean is greater than the median, which is 12. If we increase the mean to 13, we can solve for y:
(11+11+13+15+17+y)/6 = 13
67 + y = 78
y = 11
However, this would make the mode 11 as well, so it doesn't meet the unique requirement. Let's increase the mean to 14 and solve for y:
(11+11+13+15+17+y)/6 = 14
67 + y = 84
y = 17
Now, the mode, median, and mean are unique and form an increasing arithmetic sequence (11, 12, 14). Therefore, the greatest possible value of y is 17.
learn more about data here : brainly.in/question/48902948
#SPJ11
An aeroplane flew 500 km south, then 600 km east. Give its true bearing from its starting point to the nearest degree.
Answers
Answer:
Solution:
The vector diagram for various velocities is shown.Vector AC gives velocity of aeroplane relative to quiet air.Vector CB gives velocity of wind(air) relative to ground.Vector AB gives velocity of plane relative to ground.Using law of sines for triangle,
sin30
0
150
=
sinθ
20
.
Therefore,sin(θ)=
300
20
=
15
1
. Then,
Theta=sin
−1
15
1
=3.8
0
.
Angle NAC=33.8
0
.The pilot should head the plane in the direction 33.8
0
east of north
Step-by-step explanation:
WAS THIS ANSWER HELPFUL?
MARK ME AS A BRAINLIEST

Solve for x. Help Help Help Help Help, I tried dividing 17/2 which gave me 8.5 but it’s wrong

Answers
Answer:
x = 15.9
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem
a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse
6^2 + x^2 = 17^2
36+ x^2 = 289
x^2 = 289-36
x^2 =253
Take the square root of each side
sqrt(x^2) = sqrt( 253)
x = 15.90597
Rounding to the nearest tenth
x = 15.9
Determine if 0.528176817681768176 is rational or irrational
Answers
0.528176817681768176 is a rational number as it is non terminating but repeating decimal number.
A rational number is a number that can be expressed in the form of p / q where q is not equal to 0.
It can be terminating or non terminating but repeating number.
We are given a decimal number:
0.528176817681768176
We can see that, after .52, the digits 8176 keeps on repeating itself.
So, the number can also be written as:
0.528176 ( bar on 8176)
This means that the decimal number that is given is a non terminating but repeating rational number.
Therefore, 0.528176817681768176 is a rational number as it is non terminating but repeating decimal number.
Learn more about rational number here:
https://brainly.com/question/12088221
#SPJ9
what 9999999999999999999x99999999999999999999
i need help plz
Answers
Answer:
1e+39
Step-by-step explanation:
Let F: ]0, +[infinity][R → R be the function F(x, y)=y(e**y +x) - In(x). Show: there exists a neighborhood I c R of the point x0 = 1 and a unique function f :1 →R such that. (1) f(1) = 0 and f e C1(1), (2) F(x, f(x)) = 0 for all x el. (fe C1(1), means that f is differentiable and that the derivative is continuous. )
Answers
The proof of the statement, that the existence and uniqueness of the function f in the neighborhood I around x₀ = 1, satisfying the given conditions is shown below.
In order to show the existence and uniqueness of the function f, we will use the steps in the question,
Step 1: Define the neighborhood I around x₀ = 1.
Let us consider I as an interval around x₀ = 1, such as I = ]0, 2[,
Step 2: Define the function f : I → R.
We define the function f(x) as the solution to equation F(x, y) = 0 for each x in the interval I, In other words, f(x) satisfies y(\(e^{y}\) + x) - ln(x) = 0,
Step 3: Show f(1) = 0 and f ∈ C₁(1).
First, we check f(1) = 0 by substituting x = 1 into the equation:
We get, f(1) = 0(e⁰ + 1) - ln(1) = 0 - 0 = 0, which satisfies the condition.
Next, to show that f is differentiable and its derivative is continuous at x = 1, we differentiate equation F(x, y) = 0 with respect to y,
\(e^{y}\) + y(\(e^{y}\) + x) - 1/x = 0,
By solving this equation for dy/dx,
We get,
dy/dx = (1 - \(e^{y}\)) / (\(e^{y}\) + x),
Now, substitute x = 1 and y = 0 into the expression above:
dy/dx = (1 - e⁰) / (e⁰ + 1) = 0/2 = 0,
Since the derivative dy/dx is constant and equal to zero, f'(1) = 0, satisfying the condition of f being differentiable at x = 1.
Step 4: Show F(x, f(x)) = 0 for all x ∈ I.
By substituting f(x) into the equation F(x, y) = 0, We have:
f(x)(\(e^{f(x)}\) + x) - ln(x) = 0,
Since f(x) is defined as the solution to this equation, F(x, f(x)) = 0 holds for all x in the interval I.
Therefore, we have proved the existence and uniqueness of the function f in the neighborhood I around x₀ = 1, satisfying the conditions (1) and (2).
Learn more about Neighborhood here
https://brainly.com/question/31400574
#SPJ4
The given question is incomplete, the complete question is
Let F: ]0, +∞[ × R → R be the function F(x, y)=y(e**y + x) - In(x).
Show: there exists a neighborhood "I" ⊂ R of the point x₀ = 1 and a unique function f : I →R such that.
(1) f(1) = 0 and f e C₁(1),
(2) F(x, f(x)) = 0 for all x ∈ l. (f ∈ C₁(I), means that f is differentiable and that the derivative is continuous)
For a standard normal distribution (u=0, 0=1), the area under the curve less than 1.25 is 0.894. What is the approximate percentage of the area under the curve less than -1.25? 0.894 0.394 0.211 0.106
Answers
After considering all the given data we conclude that approximate percentage of area under the curve is 10.6%, which is approximately 0.106 as a decimal or 53/500 as a fraction
In case of standard normal distribution, the area under the curve less than 1.25 is 0.894.
Then the standard normal distribution is symmetric about the mean, the area under the curve less than -1.25 is the same as the area under the curve greater than 1.25.
Hence, the approximate percentage of the area under the curve less than -1.25 is approximately
(1 - 0.894) * 100% = 10.6%,
which is approximately 0.106 as a decimal or 53/500 as a fraction
To learn more about standard normal distribution
https://brainly.com/question/26822684
#SPJ4