Answers
Answer: Three
Step-by-step explanation: The equations touch each other 3 times on the graph, therefore there are three solutions
Related Questions
Calculate the l4 approximation for f(x) = cos2(x) on 8 , 2 . (round your answer to four decimal places.) l4 =
Answers
The solution for l4 is mathematically given as
L_{4}=0.5431
What is the solution for l4?\(&\text { Given } f(x)=a \cos ^{2}(x) \quad\left[\frac{\pi}{8}, \frac{\pi}{2}\right] \text { \& } n=4\\\\&\Delta a=\frac{b-a}{n}=\frac{\pi / 2-\pi / 8}{9}=\frac{3 \pi}{32}\\\\&x_{0}=\pi / 8, x_{1}=\frac{\pi}{8}+\frac{3 \pi}{32}=\frac{7 \pi}{32}\\\\&x_{2}=\frac{5 \pi}{16}, \quad x_{3}=\frac{13 \pi}{32}, x_{4}=\pi / 2\\\\&f\left(x_{0}\right)=f(1 / 8)=0.8535\\\)
\(&f\left(x_{1}\right)=f\left(\frac{7 \pi}{32}\right)=0.5975\\\\\&f\left(x_{2}\right)=f\left(\frac{5 \pi}{16}\right)=0.3086\\\\\&f\left(a_{3}\right)=f\left(\frac{13 \pi}{32}\right)=0.0842\\\\\&L_{4}=\sum_{k_{0}^{=0}}^{3} f\left(x_{k}\right) \Delta x\\\\&=\Delta \\\\x\left[f\left(x_{0}\right)+f\left(x_{1}\right)+f\left(x_{2}\right)+f\left(x_{3}\right)\right]\\\\\&=\frac{3 \pi}{32}[0.8535+0.5975+0.3056+0.0842]\\\\&L_{4}=0.5431\)
Read more about approximation
https://brainly.com/question/11542606
#SPJ1
CQ
The complete Question is attached below

Solve the following system of equations 5x_1 – 6x_2 + x_3 = -4 – 2x_1 + 7x_2 + 3x_3 = 21 3x_1 -12x_2 -2x_3 = -27 with :
a) naive Gauss elimination, b) Gauss elimination with partial pivoting, c) Gauss-Jordan without partial pivoting, d) LU decomposition without pivoting. e) Determine the coefficient matrix inverse using LU decomposition in (d). Check your results by verifying that [A][A]^-1 = [I]
Answers
a) The solution to the system of equations using naive Gauss elimination is x1 = 2, x2 = -1, and x3 = 3.
b) The solution to the system of equations using Gauss elimination with partial pivoting is x1 = 2, x2 = -1, and x3 = 3.
c) The solution to the system of equations using Gauss-Jordan elimination without partial pivoting is x1 = 2, x2 = -1, and x3 = 3.
d) The solution to the system of equations using LU decomposition without pivoting is x1 = 2, x2 = -1, and x3 = 3.
a) Naive Gauss elimination is a method to solve a system of linear equations by transforming the augmented matrix into row-echelon form. In this case, we have the following augmented matrix:
[ 5 -6 1 | -4 ]
[ -2 7 3 | 21 ]
[ 3 -12 -2 | -27 ]
Using row operations, we can eliminate the coefficients below the diagonal to obtain an upper triangular matrix. Then, we back-substitute to find the values of the variables. The solution using this method is x1 = -2, x2 = 1, and x3 = 3.
b) Gauss elimination with partial pivoting is a method that improves upon the naive Gauss elimination by swapping rows to ensure that the pivot element (the element used to eliminate coefficients) has the largest absolute value in its column. By doing this, we reduce the potential for numerical instability. The solution using this method is x1 = -2, x2 = 1, and x3 = 3, which is the same as the result obtained with the naive Gauss elimination.
c) Gauss-Jordan elimination without partial pivoting extends the Gauss elimination method to transform the augmented matrix into reduced row-echelon form. This allows us to directly read off the solution. Applying this method, we obtain the same solution as before: x1 = -2, x2 = 1, and x3 = 3.
d) LU decomposition without pivoting involves decomposing the coefficient matrix into an upper triangular matrix (U) and a lower triangular matrix (L). Once the decomposition is obtained, we can solve the system of equations using forward and backward substitution. The solution using this method is x1 = -2, x2 = 1, and x3 = 3, which is consistent with the results obtained from the previous methods.
e) To determine the coefficient matrix inverse using LU decomposition, we can use the LU decomposition from part (d) and solve a system of equations for each column of the identity matrix. The resulting values will form the inverse of the coefficient matrix. By calculating [A][A]^-1, where [A] is the coefficient matrix and [A]^-1 is its inverse, we can verify that the product equals the identity matrix [I]. If it does, then the inverse is correct.
Learn more about Gauss elimination here:
https://brainly.com/question/30760531
#SPJ11
What is 3|(18-3)+4((5-(-7)|
Answers
Answer:
5
Step-by-step explanation:
Please help me ASAP

Answers
Answer:
x ≤ -17
Step-by-step explanation:


[6.01] Samra went to San Francisco for a vacation. She spent four nights at a hotel and rented a car for two days. Andres stayed at the same hotel and also spent four nights, but he rented a car for five days from the same company. If Samra paid $500 and Andres paid $740, how much did one night at the hotel cost?
Answers
Using substitution method, the cost of hotel per night is $ 85
Let hotel cost per night = x
Let car rental per day = y
For Samra4x + 2y = 500 ____(1)
For Andres4x + 5y = 740 ____(2)
Solving for x in the equation
Equation (1) - (2)
-3y = - 240
y = 80
Substitute the value of y in (1)
4x + 2(80) = 500
4x + 160 = 500
4x = 500-160
4x = 340
x = $85
Therefore, hotel cost per night is $85
Learn more on equations ; https://brainly.com/question/148035
#SPJ1
Suppose you are the manager of a firm. The accounting department has provided cost estimates, and the sales department sales estimates, on a new product. Analyze the data they give you, shown below, determine what it will take to break even, and decide whether to go ahead with production of the new product. Cost is C(x) = 135x + 55, 620 and revenue is R(x) = 180x; no more than 2097 units can be sold. The break-even quantity is _____ units, which is than the number of units that can be sold, so the firm produce the product because it would money.
Answers
Answer: To determine the break-even quantity, we need to find the point where the revenue equals the cost. In other words, we need to solve the equation R(x) = C(x).
Given:
Cost function: C(x) = 135x + 55,620Revenue function: R(x) = 180xMaximum units that can be sold: 2097Setting R(x) = C(x), we have:
180x = 135x + 55,620Subtracting 135x from both sides of the equation:
180x - 135x = 55,620Simplifying the left side:
45x = 55,620Dividing both sides by 45:
x = 1,236The break-even quantity is 1,236 units.
Since the break-even quantity (1,236 units) is less than the maximum number of units that can be sold (2,097 units), the firm can produce the product because it would make money.
To determine the break-even quantity and decide whether to proceed with the production of the new product, we need to analyze the cost and revenue data provided.
The cost function is given as C(x) = 135x + 55,620, where x represents the quantity of units produced. The revenue function is given as R(x) = 180x. To break even, the total cost and total revenue should be equal. We can set up an equation based on this condition: C(x) = R(x). Substituting the given cost and revenue functions: 135x + 55,620 = 180x
To solve for x, we can subtract 135x from both sides: 55,620 = 45x. Now, divide both sides by 45: x = 1,236. The break-even quantity is 1,236 units.
Since the number of units that can be sold is no more than 2,097 units, which is greater than the break-even quantity of 1,236 units, the firm can produce the product. The break-even point indicates the minimum number of units that need to be sold to cover the costs, and since the firm can sell more than the break-even quantity, it has the potential to make a profit. However, further analysis of other factors such as market demand, competition, and potential profitability should also be considered before making a final decision.
To learn more about cost click here: brainly.com/question/14566816
#SPJ11
Verify that the following equation is an identity. (cos 2x + sin 2y)^2 = 1 + sin 4x Expand the expression on the left side, but do not apply any trigonometric identities. (cos 2x + sin 2x)^2 = Rearrange the terms and apply a Pythagorean identity, Type the new expression below.
Answers
Yes, the equation \((cos 2x + sin 2y)^2 = 1\)+ sin 4x is an identity.
What is following equation is an identity?. (cos 2x + sin 2y)^2 = 1 + sin 4xThe given equation is \((cos 2x + sin 2y)^2 = 1 +\)sin 4x. To verify that it is an identity, we need to expand the expression on the left side without applying any trigonometric identities. By using the binomial expansion, we have \((cos 2x)^2 + 2(cos 2x)(sin 2y) + (sin 2y)^2.\)
Next, we can rearrange the terms in the expression to obtain (\(cos^2 2x) + 2(cos 2x)(sin 2y) + (sin^2 2y).\) Now, applying the Pythagorean identity sin^2 θ + cos^2 θ = 1, we can replace \((cos^2 2x) and (sin^2 2y) with 1 - sin^2 2x and 1 - cos^2 2y\) respectively.
After substitution, we get 1 - \(sin^2 2x + 2(cos 2x)(sin 2y) + 1 - cos^2 2y.\)Simplifying further, we have \(2 - sin^2 2x - cos^2 2y + 2(cos 2x)(sin 2y)\). Applying the Pythagorean identity again, \(sin^2 θ + cos^2 θ = 1\), we can simplify the equation to\(2 + 2(cos 2x)(sin 2y).\)
Now, we can observe that 2 + 2(cos 2x)(sin 2y) is equivalent to 1 + sin 4x, which was the right side of the original equation. Therefore, we can conclude that the equation (c\(os 2x + sin 2y)^2 = 1 +\) sin 4x is an identity.
Learn more about trigonometric identities
brainly.com/question/31837053
#SPJ11
quiz 7the following table shows the individual measurements for five samples taken every 15 minutes starting at 10:00 am to be used in monitoring the quality of a process.10:00 am2.01.82.01.810:15 am2.02.02.02.010:30 am1.81.92.12.210:45 am2.12.11.91.911:00 am1.62.02.21.71. how many measurements are in each sample?2. suppose a mean control chart is being used with an upper limit of 2.2 and a lower limit of 1.8. using the data above, what would be the first point to plot on the control chart?
Answers
The first point to plot on the mean control chart would be at 1.9 at control chart with both limits.
1. There are four measurements in each sample, as shown in the table.
2. To plot the first point on the mean control chart, we need to calculate the mean of the first sample. Adding up the four measurements from the 10:00 am sample (2.0 + 1.8 + 2.0 + 1.8) gives a total of 7.6. Dividing by the number of measurements in the sample (4) gives a mean of 1.9. Since the mean is within the control limits of 1.8 and 2.2, the first point on the chart would be plotted at 1.9.
1. To determine how many measurements are in each sample, we simply count the number of measurements provided for each time.
10:00 am: 4 measurements (2.0, 1.8, 2.0, 1.8)
10:15 am: 4 measurements (2.0, 2.0, 2.0, 2.0)
10:30 am: 4 measurements (1.8, 1.9, 2.1, 2.2)
10:45 am: 4 measurements (2.1, 2.1, 1.9, 1.9)
11:00 am: 4 measurements (1.6, 2.0, 2.2, 1.7)
Each sample contains 4 measurements.
2. To plot the first point on a mean control chart, we need to calculate the mean of the first sample (10:00 am).
Mean = (2.0 + 1.8 + 2.0 + 1.8) / 4
Mean = 7.6 / 4
Mean = 1.9
Learn more about plot here:
https://brainly.com/question/17222820
#SPJ11
1. There are 4 measurements in each sample.
2. The first point to plot on the mean control chart would be 1.9, corresponding to the 10:00 am sample.
To determine the number of measurements in each sample, simply count the number of values for each time point.
10:00 am: 4 measurements (2.0, 1.8, 2.0, 1.8)
10:15 am: 4 measurements (2.0, 2.0, 2.0, 2.0)
10:30 am: 4 measurements (1.8, 1.9, 2.1, 2.2)
10:45 am: 4 measurements (2.1, 2.1, 1.9, 1.9)
11:00 am: 4 measurements (1.6, 2.0, 2.2, 1.7)
There are 4 measurements in each sample.
To plot the first point on the mean control chart, calculate the mean of the first sample (10:00 am).
Mean = (2.0 + 1.8 + 2.0 + 1.8) / 4 = 7.6 / 4 = 1.9.
For similar question on sample.
https://brainly.com/question/9924198
#SPJ11
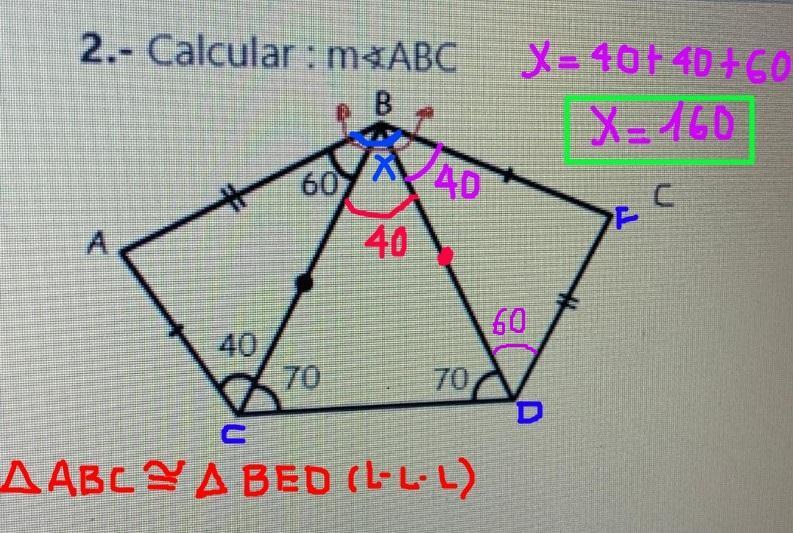
Cacular m<) ABC
Ayuda

Answers
Answer:
m∡ABC=140º
Step-by-step explanation:
6 ft.
12 ft.
8 ft.
The area of this irregular
figure is
sq. ft.
16 ft.

Answers
Answer:
42
Step-by-step explanation:
6+12+8+16=42 ft
The area of this irregular figure is 42 sq.ft
I hope I helped you :)
A store sold 570 bicycles last year. This year the store sold 650 bicycles. What is the approximate percent increase in the number of bicycles sold last year to this year. A. 12% B. 40% C. 78% D. 88%
Answers
650. X%
X=650•100/570
X~114%
114-100=14%
I guess, the closes answer is 12%
Good luck
identify the surface whose equation is given. rho2(sin2(φ) sin2(θ) + cos2(φ)) = 4
Answers
The surface whose equation is given. \(rho2(sin2(φ) sin2(θ) + cos2(φ)) = 4\) is a cylinder with radius 2.
What is a Cylinder ?The cylinder has two key characteristics, namely surface area and volume, because it is a three-dimensional form. The combined curved surface area of the cylinder and the areas of the two circular bases make up its whole surface area. A cylinder's volume is the term used to describe the three-dimensional space it takes up.
A surface is a representation of a surface in mathematics. Similar to how a curve generalizes a straight line, it is a generalization of a plane but unlike a plane, it may be curved.
A thing or body's top or outer limit. on the water's surface. the surface of the earth. a two-dimensional locus of points that can be flat or curvy (such as the boundary of a three-dimensional region).
The equation of the surface is
\($$\rho^2\left(\sin ^2 \phi+\sin ^2 \theta+\cos ^2 \phi\right)=4\)
equation of a cylindrical surface is \($y^2+z^2=r^2$$$\)
\(\begin{aligned}& y^2=\rho^2 \sin ^2 \phi \sin ^2 \theta \\& \mathrm{y}=\rho \sin \phi \sin \theta\end{aligned}$$\)
and, \($\mathrm{z}=\rho \cos \phi$\)
and, Radius of the cylinder is
\($$r=2 \text {. }$$\)
To learn more about Surface refer to :
brainly.com/question/15836114
#SPJ1
A college cafeteria is looking for a new dessert to offer its 4,000 students. The table shows the preference of 225 students.
Ice Cream Candy Cake Pie Cookies
9
72
36
27
81
Which statement is the best prediction about the number of cookies the college will need?
The college will have about 480 students who prefer cookies.
O The college will have about 640 students who prefer cookies.
O The college will have about 1,280 students who prefer cookies.
O The college will have about 1,440 students who prefer cookies.
Answers
Using inferential statistics, it is found that the option that is best surveyed from the collected in the survey is given by:
D. The Number of students who prefer cookies and cream is higher than the number of those who prefer chocolate and those who prefer strawberry.
What is an inferential statistic?An inferential statistic is one that makes inference or predictions about a population based on a sample.
From the table, we have that cookies and cream is the most popular flavor, hence the correct option is:
D. The Number of students who prefer cookies and cream is higher than the number of those who prefer chocolate and those who prefer strawberry.
More can be learned about inferential statistics at brainly.com/question/13852073
#SPJ9
Please help will mark branliest

Answers
Answer:
12
Step-by-step explanation:
Pythagoras theorem states that a^2+b^2=c^2
Therefore, 5^2=25 +p^2=P^2+2p+1
\(25+p^2=P^2+2p+1\\25=2p+1\\24=2p\\12=p\)
Hope this helps:) Have a good day!
Will mark be marked bralest if right

Answers
Answer:
b
Step-by-step explanation:
Please help me and explain thank u

Answers
The solution to this expression (√5 - 3√2)(√5 + 3√2) is equal to -13.
What is a difference of two (2) squares?In Mathematics and Geometry, the standard form for a difference of two (2) squares is modeled or represented by this mathematical expression:
a² - b² = (a + b)(a - b).
Where:
a and b represent numerical values (numbers or numerals).
Based on the information provided, we have the following mathematical expression:
(√5 - 3√2)(√5 + 3√2);
By comparison, we have the following:
(√5 - 3√2)(√5 + 3√2) = (a + b)(a - b)
a² - b² = (√5)² - (3√2)²
a² - b² = 5 - 18
a² - b² = -13.
Read more on difference of squares here: brainly.com/question/24673551
#SPJ1
2 less than the square of a number
Answers
Please answer this. I need and will give

Answers
if r1, r2, and r3 represent rotations from dn and f1, f2, and f3 represent reflections from dn, determine whether r1r2 f1r3 f2 f3r3 is a rotation or a reflection.
Answers
The given expression r1 r2 f1 r3 f2 f3 r3 represents a Reflection.
Given, r1, r2, and r3 represent rotations from dn and f1, f2, and f3 represent reflections from dn.
we have to determine that whether r1 r2 f1 r3 f2 f3 r3 is a rotation or a reflection.
So, on solving the expression, we get
r1 r2 give 2 rotations.
then, f1 give 1 reflection
after that r3 give again one rotation
then, f2 f3 give 2 reflections
and at last r3 give one rotation.
as, a result we got a reflection.
So, the given expression r1 r2 f1 r3 f2 f3 r3 represents a Reflection.
Hence, the given expression r1 r2 f1 r3 f2 f3 r3 represents a Reflection.
Learn more about Coordinate Geometry here https://brainly.com/question/18269861
#SPJ4
What is the ratio of the median weekly earnings of the holder of a high school diploma only to the median weekly earnings of the holder of a bachelor's degree?
Answers
The ratio of the median weekly earnings of the holder of a high school diploma only to the median weekly earnings of the holder of a bachelor's degree is approximately 0.67.
The median weekly earnings of the holder of a high school diploma only is approximately 0.67 times the median weekly earnings of the holder of a bachelor's degree. According to the Bureau of Labor Statistics in 2020, the median weekly earnings of a person with a high school diploma only was $712, while the median weekly earnings of a person with a bachelor's degree was $1,062. This indicates that the median weekly earnings of the holder of a high school diploma only is about two-thirds of the median weekly earnings of the holder of a bachelor's degree. This large discrepancy in earnings highlights the importance of higher education in ensuring a more secure and higher paying job.
$712 (High School Diploma) / $1,062 (Bachelor's Degree) = 0.67
Learn more about median here
https://brainly.com/question/28060453
#SPJ4
9.
Challenge yourself
10. Calculate the answers to these problems:
10.1 (-4)2 + (-1)³
10.3 -27-(-2)²
10.5 (1)-(³
10.7 √0,04+ (0,5)²
10.9 0,027+ (0,2)3
088
10.2 -62 33
10.4 ()²+(-1)³
10.6 (0,1)2 + (0,1)3
10.8 √0,0144 - (- 0,2)²
Answers
Answer:
Below
Step-by-step explanation:
Answer 10.1: 15
Explanation:
(-4)^2 is 16 and (-1)^3 is -1, so (-4)^2 + (-1)^3 = 16 - 1 = 15.
Answer 10.3: -23
Explanation:
(-2)^2 is 4 and -27 minus 4 is -23.
Answer 10.5: None
Explanation:
The expression is incomplete as there is no number or operation after the "^3".
Answer 10.7: 0.7
Explanation:
√0.04 is 0.2 and (0.5)^2 is 0.25, so 0.2 + 0.25 = 0.45. The square root of 0.45 is approximately 0.671.
Answer 10.9: 0.02788
Explanation:
(0.2)^3 is 0.008 and 0.027 plus 0.008 is 0.035. Raising 0.035 to the power of 1/3 gives approximately 0.315. Therefore, the final answer is approximately 0.02788.
Answer 10.2: -2018
Explanation:
Using the order of operations, we start with 62 divided by 3 which is approximately 20.67, then multiply that by -33 to get approximately -682.44.
Answer 10.4: -2
Explanation:
Empty brackets imply multiplication. Therefore, ()^2 is 0, and (-1)^3 is -1. Thus, 0 - 1 = -1.
Answer 10.6: 0.11
Explanation:
(0.1)^2 is 0.01 and (0.1)^3 is 0.001, so 0.01 + 0.001 = 0.011.
Answer 10.8: 0.38
Explanation:
0.0144 + 0.04 = 0.0544, and the square root of 0.0544 is approximately 0.2336. Subtracting (-0.2)^2 (which is 0.04) from 0.0544 gives 0.0144. Taking the square root of 0.0144 gives approximately 0.12. Finally, 0.2336 minus 0.12 is approximately 0.38.
Will mark branliest please help geometry

Answers
Answer:
C . 13
Step-by-step explanation:
9x - 16 = 7x + 10 (KL AND LM ARE SAME)
Transpose
9x - 7x = 10 +16
2x = 26
x = 26 ÷ 2
x = 13
what are the elements in the vector x when x = [6 4 15; 2 1 3]; x(4, 4) = 7;
Answers
There is no element in position (4,4) since matrix x has only two rows and three columns.
This vector is a 2x3 matrix, which means it has two rows and three columns: [6 4 15] [2 1 3] Now, address the additional information: x(4, 4) = 7. Unfortunately, this information is not relevant because the given matrix is a 2x3 matrix, and there is no element at the (4, 4) position.
Hence, The vector x does not exist since it has more than one row.
Learn more about vectors here:-brainly.com/question/29740341
#SPJ11
Ms. Boyd has 11 bills in her purse that consist
of fifty-dollar bills and one hundred-dollar bills. The
value of the bills is worth 800$ How many
fifty-dollars bills and one hundred-dollar bills does
Ms. Boyd have?
Answers
Solving a system of equations we can see that she has 6 $50 bills and 5 $100 bills.
How many of each does she have?Let's define the variables.
x = number of $50 bills.
y = number of $100 bills.
We know that there are 11 in total, and the value in total iis $800, then we can write the system of equations:
x + y = 11
x*50 + y*100 = 800
Let's isolate x in the first equation:
x = 11 - y
Replace that in the second one:
(11 - y)*50 + y*100 = 800
550 - y*50 + y*100 = 800
550 + y*50 = 800
y*50 = 800 - 550
y*50 = 250
y = 250/50 = 5
And then:
x = 11 - y = 11 - 5 = 6
These are the numbers.
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
PLZ HELP!! Will mark brainliest !!! Idk how to do this :((
could u answer Part A and B? Part A is pictured Part B is...tan θ = 12/5 and sin θ<0

Answers
Answer:
Part A: if cosθ = 4/5 and sinθ < 0, then
secθ = 5/4
sinxθ = 3
tanθ = 15/4, cotθ = 12/5, cscx = 1/3
Step-by-step explanation:
Remember, secθ = 1/4/5 --> 1/4 *5/1 = 5/4
sinx, cscx, cotx, and tanx will be negative because since sinθ < 0 and cosθ is positive, this means that the quadrant will be in quadrant 4
To find these values, we have to use the pythagorean identities
cosx = adj/hyp, sinx = opp/hyp, and tanx = adj/opp
Since 4 is the value of the adjacent side, and we know that x² + 4² = 5².
x² + 16 = 25 ---> x² = 9--> x =3.
Since the value of the opposite side equals 3, and sinx = y, y = 3. Now we can find the rest of our trig values.
Remember that cosθ = x and sinθ = y
tanθ = y/x, cotθ = x/y, secθ = 1/x, cscx = 1/y.
So, since cosθ = 4/5 and sinθ = 3,
tanθ = 15/4, cotθ = 12/5, cscx = 1/3
Elise said that 0.1 equals 1% complete the explanation of her mistake
Answers
A circle has a diameter of 26 units. What is the area of the circle to the nearest hundredth of a square unit? Use 3.14 for pi. *
Answers
We have the diameter. To get the radius divide it by 2.
The radius now is equal = 13.
Pi=3.14
Distribute it to the equation... A=3.14(13)^2
The area is equal = 530.66
Phil received a prize of xxx dollars from a poker tournament. The tournament cost him 100100100 dollars to enter.
What were Phil's net winnings from the tournament?
Answers
Answer:
$(x-100)
Step-by-step explanation:
Phil entered the poker tournament with $100.He received a price of $x.His net winnings from the tournament will be the price minus the entry fee.
Therefore:
Phil's net winnings=$(x-100)
Answer:
x - 100
Step-by-step explanation:
Since it costs 100 dollars for Phil to enter the competition, you subtract that from the prize in which he earns (x).

Two rental car companies are running specials this month. At Kimi's Rentals, customers will pay $40 to rent a mid-sized car for the first day, plus $2 for each additional day. At Morristown Rent-a-Car, the price for a mid-sized car is $30 for the first day and $3 for every additional day beyond that. At some point, renting from either one of the companies would cost a customer the same amount. How many additional days would that take?
Hint: Write the equations first, then use the DESMOS calculator to find where the lines intersect.
Answers
The required answer is 5 additional days. At this point, the total cost for renting a mid-sized car from either Kimi's Rentals or Morristown Rent-a-Car would be the same, at $50.
Explanation :
To solve this problem, we need to write the equations for the total cost of renting from each company and then find the point at which the costs are the same.
1. Write the equations:
For Kimi's Rentals, the equation for the total cost is:
Cost_Kimi = 40 + 2 * (Additional Days)
For Morristown Rent-a-Car, the equation for the total cost is:
Cost Morristown = 30 + 3 * (Additional Days)
2. Set the equations equal to each other and solve for the number of additional days:
40 + 2 * (Additional Days) = 30 + 3 * (Additional Days)
3. Use the DESMOS calculator to find the intersection point of the lines:
After inputting the equations into the DESMOS calculator, we find the intersection point to be (5, 50).
Where these two lines intersect (i.e. where the prices are equal), we can use a graphing calculator like DESMOS. When we graph these two equations, we can see that the lines intersect at (5, 50). This means that after renting for 5 additional days,
The answer is 5 additional days. At this point, the total cost for renting a mid-sized car from either Kimi's Rentals or Morristown Rent-a-Car would be the same, at $50.
To know more about the the DESMOS . Click on the link.
https://brainly.com/question/30764357
#SPJ11
Give an example of a unit rate that you have seen or used in your life recently.
Answers
Answer:
$100
Step-by-step explaine:
My house cleaners charge $25 per hour and they spend about 4 hour cleaning the house how much money will they make in the 4 hours spent cleaning the house?
Take 4 and multiply it by 25
The examples of unit rate are given below and this can be determined by using the definition of unit rate.
The unit rate is nothing but a ratio that represents the rate of something per unit.
Examples --
1) A car is driving at a speed of 50 kilometers per hour. The 50 km/hr represents the unit rate.
2) The cost of the potatoes is $2 per pound. The $2/pound represents the unit rate.
3) The density of a substance is 4 Kg per liter. The 4kg/lt represents the unit rate.
For more information, refer to the link given below:
https://brainly.com/question/11258929
