f r=9, b=5, and g=−6, what does (r+b−g)(b+g) equal?
-20
-8
8
19
20
Answers
Answer:
-20
Step-by-step explanation:
=(9+5-(-6)) (5+(-6))
=(20) (-1)
=-20
Related Questions
What does a positive times a negative times a negative equal?
Answers
Answer:
A positive.
Step-by-step explanation:
Remember that there is an even amount of negatives in this situation which makes it a positive. Two positive numbers multiplied together are still positive.
positive x negative = negative
negative x negative = positive
if you need to go further you just keep going with the thought that it's positive unless the signs are different
grandma loves to read about the weather
Answers
I hate my grandma I hope she goes to hell but lucky for her she is Christian.
i need to find the slope like asap help thanks
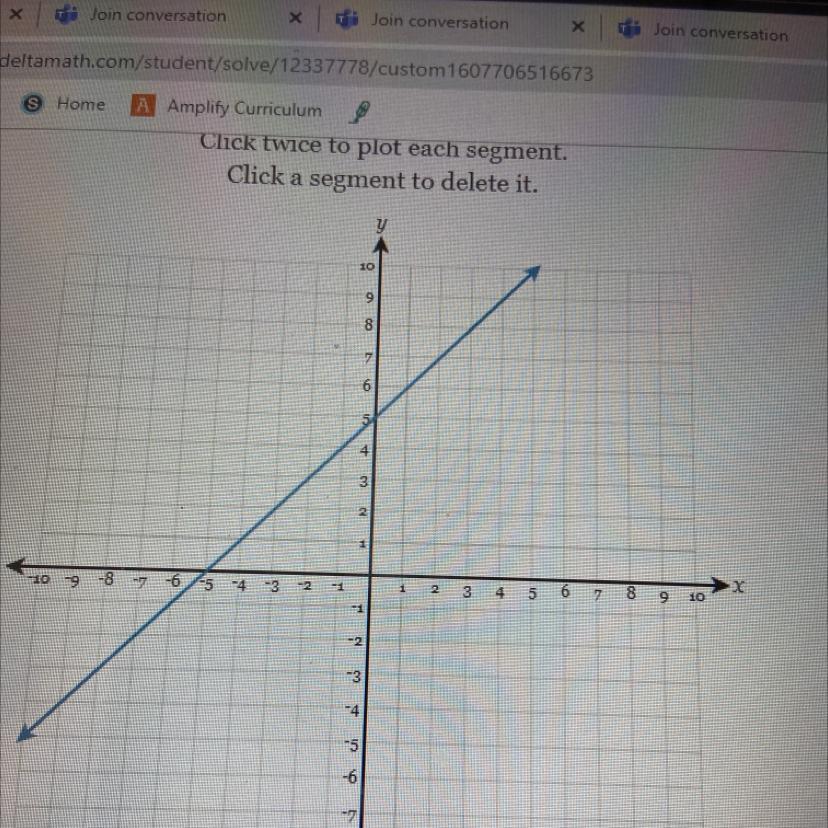
Answers
Answer:
1
Step-by-step explanation:
Using a slope triange we can see that the rise is 1 and the run is 1 and 1/1=1
A firm has the total cost function TC=120+45Q-Q^2+0.4Q^3 and faces a demand curve given P=240-20p what is the profit
Answers
Step-by-step explanation:
To find the profit of the firm, we need to first determine the quantity Q that maximizes the profit, and then use that quantity to find the price and profit.
The profit function can be written as:
π(Q) = TR(Q) - TC(Q)
where TR(Q) is the total revenue function and TC(Q) is the total cost function. We can write TR(Q) as:
TR(Q) = P(Q) * Q
where P(Q) is the price function, which is given as:
P(Q) = 240 - 20Q
So, the profit function becomes:
π(Q) = (240 - 20Q) * Q - (120 + 45Q - Q^2 + 0.4Q^3)
Simplifying this expression, we get:
π(Q) = -0.4Q^3 + 24.6Q^2 - 195Q + 120
To maximize the profit, we take the derivative of the profit function with respect to Q and set it equal to zero:
π'(Q) = -1.2Q^2 + 49.2Q - 195 = 0
Solving for Q using the quadratic formula, we get:
Q = (49.2 ± sqrt(49.2^2 - 4*(-1.2)(-195))) / (2(-1.2))
Q = 21 or Q = 32.5
Since the coefficient of the Q^3 term in the profit function is negative, the profit function has a maximum at Q = 32.5. Therefore, the firm should produce and sell 32.5 units of output.
To find the price that the firm should charge, we substitute Q = 32.5 into the demand function:
P = 240 - 20Q
P = 240 - 20(32.5)
P = 160
Therefore, the firm should charge a price of $160 per unit.
To find the profit at the optimal level of output, we substitute Q = 32.5 and P = 160 into the profit function:
π(Q) = -0.4Q^3 + 24.6Q^2 - 195Q + 120
π(32.5) = -0.4(32.5)^3 + 24.6(32.5)^2 - 195(32.5) + 120
π(32.5) = $1,722.81
Therefore, the profit at the optimal level of output is $1,722.81
Can someone help me with this pleaseeeeee

Answers
The values of x, y , and z in the matrix equation is 3, 4, 0 respectively.
What is the solution of the matrix equation?The solution of the matrix equation is calculated by applying Cramer's rule as shown below;
[ 1 1 -1 ] [ 7 ]
[ 2 3 0 ] [ 18 ]
[ -5 -7 -1 ] [ -43 ]
The determinant of the matrix is calculated as follows;
[ 1 1 -1 ]
[ 2 3 0 ]
[ -5 -7 -1 ]
Δ = 1 (-3 - 0) - 1(-2 - 0 ) - 1(-14 + 15)
Δ = -2
The x determinant of the matrix is calculated as follows;
[ 7 1 -1 ]
[ 18 3 0 ]
[ -43 -7 -1 ]
Δx = 7 (-3 - 0) - 1 (-18 - 0 ) - 1(-126 + 129)
Δx = -6
The y determinant of the matrix is calculated as follows;
[ 1 7 -1 ]
[ 2 18 0 ]
[ -5 -43 -1 ]
Δy = 1 (-18 - 0 ) - 7(-2 - 0 ) -1(-86 + 90)
Δy = -8
The z determinant of the matrix is calculated as follows;
[ 1 1 7 ]
[ 2 3 18 ]
[ -5 -7 -43]
Δz = 1 (-129 + 126) - 1(-86 + 90) + 7(-14 + 15)
Δz = 0
The values of x, y , and z is calculated as;
x = Δx/Δ = -6/-2 = 3
y = Δy/Δ = -8/-2 = 4
z = Δz/Δ = 0/-2 = 0
Learn more about matrix equation here: https://brainly.com/question/11989522
#SPJ1
Certain advertisers would like to estimate the proportion of viewers who spend the majority of their television time
watching alone. The consensus is that this percentage has been increasing over the years due to the increased
number of television sets in households.
a. Determine the sample size needed to construct a 90% confidence interval with a margin of error of no more than
6% to estimate the true proportion of viewers who watch television alone.
b. What impact would a pilot sample that showed that 44% of viewers spend the majority of their television time
watching alone have on your on results.
a. The sample size needed is
(Round up to the nearest integer.)
b. The new sample size needed would be 0
(Round up to the nearest integer.)
Answers
Answer:
Step-by-step explanation:

What is the value of n?
Enter your answer in the box.
n= ____m

Answers
The value of n, considering the intersecting chords in the circle, is given as follows:
n = 6m.
What is the chord of a circle?A chord of a circle is a straight line segment that connects two points on the circle. Specifically, it is a line segment whose endpoints are on the circle. A chord is often denoted by drawing a line segment between the two endpoints, with the segment passing through the interior of the circle.
When two chords intersect each other, then the products of the measures of the segments of the chords are equal.
Considering the two intersecting chords for the circle in this problem, the value of n is obtained as follows:
5n = 15 x 2
5n = 30
n = 30/6
n = 6m.
More can be learned about the chords of a circle at https://brainly.com/question/16636441
#SPJ1
The universities budget covers cost for nine months what is Amy’s monthly budget for textbooks in course supplies? What is her monthly budget for rent on utilities and food? What is your monthly budget for a personal and miscellaneous cost? what is her total monthly budget?

Answers
We can compute Amy's monthly budget for each question using division operations, as follows:
1. Amy's monthly budget for textbooks and course supplies is $100.
2. Amy's monthly budget for rent, utilities, and food is $1,422.
3. Amy's monthly budget for personal and miscellaneous costs is $251.
4. Amy's total monthly budget is $1,825.
How to determine the monthly budget:The total monthly budget is the total budget divided by the period (nine months).
Division operations can be used to determine the individual monthly budgets for each expense class by dividing the total cost by 9.
Living On/Off-Campus:Textbooks and Course Supplies = $900 $100
Rent, Utilities, and Food = $12,798 $1,422
Personal & Miscellaneous Expense = $2,259 $251
Transportation = $468 $52
Total non-tuition expenses = $16,425 $1,825 ($16,425/9)
The number of months for the year = 9 months
Learn more about division operations at https://brainly.com/question/4721701
#SPJ1
can someone plz help with my math?!?!


Answers
Answer:
a) Plan B cost more, and $6
b) Plan B cost less according to long calls
Step-by-step explanation:
As you can see that at 175 minutes used(per month) Plan A is $14 and Plan B is $20. So Plan B cost more but the difference between then is 20 - 14 = 6. For the second question: They cost the same at 250 minutes used(per month) and Plan B since the line is flat and the price is the same for all minutes
What is the value of the expression below when y=4y=4? 3y^2 +y+8 3y 2 +y+8
Answers
Answer:
1. 18
2. 13.5
3. 3rd choice
4. 2nd choice
5. 18.6
6.3m + 8
7. 5x2 + y
i hope this work for you
Triangle ABC with vertices at A(4, 3), B(3, −2), C(−3, 1) is dilated using a scale factor of 1.5 to create triangle A′B′C′. Determine the vertex of point A′.
Answers
The vertex of point A' in the dilated triangle A'B'C' is (6, 4.5).
1. Start by calculating the distance between the vertices of the original triangle ABC:
- Distance between A(4, 3) and B(3, -2):
Δx = 3 - 4 = -1
Δy = -2 - 3 = -5
Distance = √((-\(1)^2\) + (-\(5)^2\)) = √26
- Distance between B(3, -2) and C(-3, 1):
Δx = -3 - 3 = -6
Δy = 1 - (-2) = 3
Distance = √((-6)² + 3²) = √45 = 3√5
- Distance between C(-3, 1) and A(4, 3):
Δx = 4 - (-3) = 7
Δy = 3 - 1 = 2
Distance = √(7² + 2²) = √53
2. Apply the scale factor of 1.5 to the distances calculated above:
- Distance between A' and B' = 1.5 * √26
- Distance between B' and C' = 1.5 * 3√5
- Distance between C' and A' = 1.5 * √53
3. Determine the coordinates of A' by using the distance formula and the given coordinates of A(4, 3):
- A' is located Δx units horizontally and Δy units vertically from A.
- Δx = 1.5 * (-1) = -1.5
- Δy = 1.5 * (-5) = -7.5
- Coordinates of A':
x-coordinate: 4 + (-1.5) = 2.5
y-coordinate: 3 + (-7.5) = -4.5
4. Thus, the vertex of point A' in the dilated triangle A'B'C' is (2.5, -4.5).
For more such questions on triangle, click on:
https://brainly.com/question/1058720
#SPJ8
A poster has a thickness of 1.2 x 10-2 inches.
If two posters are glued together, find the
combined thickness of the posters.
Answers
Answer:
2.4 × 10^-2
Step-by-step explanation:
You can do a sort of "undistributive" property and factor out the 10^-2 and then add the 1.2+1.2
1.2×10^-2 + 1.2×10^-2
= 10^-2(1.2 + 1.2)
= 10^-2(2.4)
= 2.4 × 10^-2
OR you can change from scientific notation to standard and add them and change back to sci. not. See image.

A firm decides to invest in a new piece of machinery which is expected to produce an
additional revenue of $8000 at the end of every year for 10 years. At the end of this
period the firm plans to sell the machinery for scrap, for which it expects to receive
$5000. What is the maximum amount that the firm should pay for the machine if it is
not to suffer a net loss as a result of this investment? You may assume that the discount
rate is 6% compounded annually.
Answers
The maximum amount the firm should pay for the machinery is $61,672.67
The maximum amount that the firm should pay for the machinery can be determined by calculating the present value of the cash flows expected from the new piece of machinery
Present value is the sum of the discounted cash flows from the investment
Discounted year 1 cash flow: $8000 ÷ 1.06 = 7547.17
Discounted year 2 cash flow: $8000 ÷ 1.06² = 7119.97
Discounted year 3 cash flow: $8000 ÷ 1.06³ = 6716.95
Discounted year 4 cash flow: $8000 ÷ 1.06^4 = 6,336.75
Discounted year 5 cash flow: $8000 ÷ 1.06^5 = 5,978.07
Discounted year 6 cash flow: $8000 ÷ 1.06^6 = 5,639.68
Discounted year 7 cash flow: $8000 ÷ 1.06 ^7= 5,3204.57
Discounted year 8 cash flow: $8000 ÷ 1.06^8 = 4,322.15
Discounted year 9 cash flow: $8000 ÷ 1.06^9 = 4,735.19
Discounted year 10 cash flow: $8000 ÷ 1.06^10 = 4,467.16
Discounted year 10 cash flow: $5000 ÷ 1.06^10 = 2,791.97
The sum of the discounted cash flows is $61,672.67
A similar question was solved here: https://brainly.com/question/17150271?referrer=searchResults
560/17 participate in a football tournament if each team plays against every other team ones, how many matches will be played tota
Answers
According to the information, it can be inferred that the total matches that would be played in total are 160,461.
What is a mathematical combination?A combination is a term to refer to an arrangement of elements in no particular order. For example:
When we put together a sandwich with salami, ham and turkey. The order in which the deli meats are placed does not matter as long as they are in a sandwich. There is only one way to stack the meat on the sandwich when the order doesn't matter.
How to calculate how many matches will be played in total?To calculate how many matches will be played in total we have to perform the following procedure:
\(= ^{567} C_{2} \\= \frac{(567)!}{2!565!} \\= \frac{567 * 566 * (565)!}{2 * (565)!} \\= 567 * 283\\= 160,461\\\\\)
As we can see after the combination, the number of games that would be played in this tournament would be 160,461.
Learn more about combination in: https://brainly.com/question/20211959
#SPJ1
1
1 point
mZABD = 79
D
C
V
(5x + 4)
(8x - 3)
В B.
A
x= type your answer...
2
1 point

Answers
Answer:
x = 6
Step-by-step explanation:
∠ DBC + ∠ ABC = ∠ ABD , substitute values
5x - 4 + 8x - 3 = 79
13x + 1 = 79 ( subtract 1 from both sides )
13x = 78 ( divide both sides by 13 )
x = 6
let d be diagonal, with repeated diagonal entries grouped contiguously. show that if a commutes with d, then it must be block diagonal.
Answers
As, a is block diagonal, with diagonal blocks of size \(m_1 \times m_1\), \(m_2 \times m_2\), \(\dots\), \(m_k \times m_k\), respectively. So, if a commutes with d, then it must be block diagonal.
Let's suppose that d is a diagonal matrix with repeated diagonal entries grouped contiguously, i.e.,
d = \(\begin{pmatrix} D_1 & 0 & 0 & \cdots & 0 \ 0 & D_1 & 0 & \cdots & 0 \ 0 & 0 & D_2 & \cdots & 0 \ \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & 0 & \cdots & D_k \end{pmatrix}\),
where \(D_1, D_2, \dots, D_k\) are scalars and appear with frequencies \(m_1, m_2, \dots, m_k\), respectively, so that \(m_1 + m_2 + \dots + m_k = n\), the size of the matrix.
Suppose that \(a\) is a matrix that commutes with d, i.e., ad = da.
Then, for any \(i \in {1, 2, \dots, k}\), we have
\(ad_{ii} = da_{ii}\)
Here, \(d_{ii}\) denotes the \(i$th\) diagonal entry of d, i.e., \(d_{ii} = D_i\) for \(i = 1, 2, \dots, k\). Since d is diagonal, \(d_{ij} = 0\) for \(i \neq j\), and
hence
\(ad_{ij} = da_{ij} = 0\)
for all \(i \neq j\).
Therefore, a is also diagonal, with diagonal entries \(a_{ii}\), and we have
\(a = \begin{pmatrix} a_{11} & 0 & 0 & \cdots & 0 \ 0 & a_{11} & 0 & \cdots & 0 \ 0 & 0 & a_{22} & \cdots & 0 \ \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & 0 & \cdots & a_{kk} \end{pmatrix}\)
Thus, a is block diagonal, with diagonal blocks of size \(m_1 \times m_1\), \(m_2 \times m_2\), \(\dots\), \(m_k \times m_k\), respectively.
Therefore, if a commutes with d, then it must be block diagonal.
For similar question block diagonal,
https://brainly.com/question/10635277
#SPJ4
There are 2 white chocolates for every plain chocolate in a box of chocolates.
There are no chocolates of any other colour in the box.
There are 10 plain chocolates in the box.
How many chocolates are there in the box altogether?
Answers
Answer:
Step-by-step explanation:
10 x 2=20 white chocolate
10+20=30 chocolates altogether
Suppose 150 mL (milliliters) of a medication is administered to an infected patient. It is estimated that 8%
of this person’s cells are infected with a virus.
1. Suppose 2 mL of the medication contains 2.3 × 103 antiviral proteins. How many antiviral proteins were
injected into this person? Express your answer in scientific notation.
2. There are about 1 × 1014 cells in the average adult human body. What percentage of this person’s cells
can be affected by the administered medication?
3. How many mL of medication would need to be administered to the patient in order to have 1 antiviral
protein for every infected cell? How many liters is this equivalent to?
Answers
Answer:
Step-by-step explanation:
To find the number of antiviral proteins injected into the person, we can set up a proportion:
2 mL contains 2.3 × 10^3 antiviral proteins
x mL contains how many antiviral proteins?
The proportion can be written as:
2 mL / 2.3 × 10^3 = x mL / (unknown number of antiviral proteins)
We can solve this proportion by cross-multiplication:
2 mL * (unknown number of antiviral proteins) = 2.3 × 10^3 antiviral proteins * x mL
x = (2.3 × 10^3 antiviral proteins * x mL) / 2 mL
Simplifying, we get:
x = 1.15 × 10^3 * x mL
Therefore, the number of antiviral proteins injected into the person is 1.15 × 10^3.
The total number of cells in the person's body is approximately 1 × 10^14. If 8% of the person's cells are infected with the virus, we can calculate the percentage of cells that can be affected by the medication:
Percentage of cells affected = (Number of infected cells / Total number of cells) * 100
Number of infected cells = 8% of 1 × 10^14 cells
Number of infected cells = (8/100) * 1 × 10^14
Number of infected cells = 8 × 10^12
Percentage of cells affected = (8 × 10^12 / 1 × 10^14) * 100
Percentage of cells affected = 8 × 10^-2 * 100
Percentage of cells affected = 8%
Therefore, the administered medication can affect 8% of the person's cells.
To find the amount of medication needed to have 1 antiviral protein for every infected cell, we can set up a proportion:
2.3 × 10^3 antiviral proteins in 2 mL
1 antiviral protein in x mL
The proportion can be written as:
2.3 × 10^3 antiviral proteins / 2 mL = 1 antiviral protein / x mL
We can solve this proportion by cross-multiplication:
(2.3 × 10^3 antiviral proteins) * x mL = 2 mL * 1 antiviral protein
x = (2 mL * 1 antiviral protein) / (2.3 × 10^3 antiviral proteins)
Simplifying, we get:
x = 0.8696 mL
Therefore, to have 1 antiviral protein for every infected cell, approximately 0.8696 mL of medication needs to be administered. This is equivalent to 0.0008696 liters.
What is the measure of angle BAC

Answers
Ignore the other questions I just need help with numbers 18 and 25 how do you work it out please help me out I would of have helped you


Answers
Answer:
25. -7/5 \(\leq\) x \(\leq\) 1
Step-by-step explanation:
18:
\(5-|x|\leq 2\\-|x| \leq -3\\|x|\leq 3\\x\geq -3\)or \(x\leq 3\)
25:
\(3|5x+1|-6\geq 12\\3|5x+1|\geq 18\\|5x+1|\geq 6\\x\leq -7/5\)or \(x\geq 1\)
\(-7/5\leq x\leq 1\)
I don't think I explained this well let me know if you need more explanation.
What is the solution of the system of equations?y = 23x + 57x – 3y = 15

Answers
Hello there. To solve this system of equations, we'll use the method of substitution.
Take the first equation, in which y = 2/3x + 5 and plug in this value of y in the second equation:
7x - 3(2/3x + 5) =15
Apply the FOIL
7x - 2x - 15 = 15
Sum 15 on both sides of the equation and add the values
5x = 30
Divide both sides of the equation by a factor of 5
x = 6
Now, plug in this value on the first equation:
y = 2/3 * 6 + 5
Multiply and add the values
y = 4 + 5 = 9
The solution to this system of equations is the pair (6, 9)
A rectangle with a perimeter of 40 inches has a width that is 3 times the length. What is the length And the width
Answers
The Length is 5 inches and the Breadth is 15 inches
What is Perimeter?
A perimeter is a closed route that covers, surrounds, or outlines a two-dimensional form or length. The circumference of a circle or an ellipse is its perimeter. There are various practical applications for calculating the perimeter.
Solution:
Perimeter of Rectangle = 2*(Length + Breadth)
According to the question
Breadth = 3*Length
Perimeter = 40
40 = 2*(Length + 3*Length)
20 = 4*Length
Length = 5 inch
Breadth = 15 inch
To learn more about Perimeter from the given link
https://brainly.com/question/19819849
#SPJ1
For the rotation -757°, find the coterminal angle from 0° ≤ 0 < 360°, the
quadrant, and the reference angle.
Answers
To find the coterminal angle for a rotation of -757°, we can add or subtract multiples of 360° until we find an angle between 0° and 360° that is coterminal with -757°.
Adding 360° multiple times:
-757° + 360° = -397° (not coterminal)
-397° + 360° = -37° (not coterminal)
-37° + 360° = 323°
Therefore, the coterminal angle for -757° is 323°.
To find the quadrant in which 323° lies, we can note that 323° is between 270° and 360°, which means it lies in the fourth quadrant.
To find the reference angle for 323°, we can subtract 360° from 323° until we get an angle between 0° and 90°:
323° - 360° = -37° (not in the correct range)
-37° + 360° = 323°
So the reference angle for 323° is 37°.
The winner of a 100 mile race drove his car to victory at a rate of 120.1229 mph. What was his time to the nearest thousandth of an hour)?
His time was hours.
(Round to the nearest thousandth.)
Answers
Answer:
\(t=1.201\ \text{hour}\)
Step-by-step explanation:
Given that,
Distance, d = 100 mile
Velocity of the winner, v = 120.1229 mph
We know that velocity of an object is equal to distance per unit time. Let t is the time. So,
\(v=\dfrac{d}{t}\\\\t=\dfrac{d}{v}\\\\t=\dfrac{120.1229}{100 }\\\\t=1.201229\ \text{hour}\\\\\text{Round to the nearest thousandth}\\\\t=1.201\ \text{hour}\)
Hence, 1.201 hour is taken by the winner.
A survey was conducted to determine the amount of time, on average, during a given week SCAD students spend outside of class on class work (projects, homework, and studying). The data shows: 5, 7, 11, 14, 18, 22 (in hours). Calculate the standard deviation by using the appropriate formula. Round your answer to three decimal places.
Answers
Answer:
Standard Deviation = 5.928
Step-by-step explanation:
a) Data:
Days Hours spent (Mean - Hour)²
1 5 61.356
2 7 34.024
3 11 3.360
4 14 1.362
5 18 26.698
6 22 84.034
6 days 77 hours, 210.834
mean
77/6 = 12.833 and 210.83/6 = 35.139
Therefore, the square root of 35.139 = 5.928
b) The standard deviation of 5.928 shows how the hours students spend outside of class on class work varies from the mean of the total hours they spend outside of class on class work.
The function f(x) = 75x + 100 models the cost of renting an event tent, where x is the number of hours and f(x) is the total cost. What is a reasonable domain for the function?
A. x < 0
B. x > 0
C. all real numbers
D. cannot be determined
Answers
The reasonable domain for the function is (b) x > 0
What is a reasonable domain for the function?From the question, we have the following parameters that can be used in our computation:
The function f(x) = 75x + 100
Where x is the number of hours
f(x) is the total cost.
In this case, the number of hours cannot be negative or 0
This means that the values of x in the function would be x > 0
These values of x are the domain
So, the reasonable domain for the function os (b) x > 0
Read more about domain at
https://brainly.com/question/27910766
#SPJ1
Simplify to a single trig function or constant with no fractions.

Answers
We can simplify cosec(t)tant(t) to sec(t). A trigonometric function is a mathematical function that relates the angles of a triangle to the ratios of its sides.
The most common trigonometric functions are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc).
To simplify the expression cosec(t)tant(t), we need to use the trigonometric identity:
cosec(t) = 1/sin(t)
tant(t) = sin(t)/cos(t)
Substituting these expressions into the original expression, we get:
cosec(t)tant(t) = (1/sin(t))(sin(t)/cos(t))
The sin(t) term in the numerator and denominator cancel out, leaving:
cosec(t)tant(t) = 1/cos(t)
Recalling the definition of secant, sec(t) = 1/cos(t), we can express the simplified expression as:
cosec(t)tant(t) = 1/sec(t)
Therefore, we can simplify cosec(t)tant(t) to sec(t).
Learn more about trigonometric identity :
https://brainly.com/question/3785172
#SPJ1
Anthony’s locker is (x+4) ft. long and (x+2) ft. wide. Area = __________________ft.^2 Letter 1: ____
Answers
What is the median of the data set below? 12, 11, 14, 14, 14, 12, 7
Answers
Median is the Middle number
1. Sort the numbers until they are all in value order
2. Find the middle number
So the answer would be 12
Answer:
Median = 12
Step-by-step explanation:
12, 11, 14, 14, 14, 12, 7
Arranging the given data in ascending order, we find:
7, 11, 12, 12, 14, 14, 14
Here,
Number of observations (N) = 7
\( \therefore \: \frac{N + 1}{2} = \frac{7 + 1}{2} = \frac{8}{2} = 4 \\ \\ median \: = 4th \: term \\ \huge \red{ \boxed{median = 12}}\)
please can someone help me with this question
The product of 7 and a number is 126. Find the number.
Answers
Answer:
18
Step-by-step explanation:
The question in algebra :
7x = 126
what is x ? :
x = 126 ÷7 (done through balancing)
x = 18
Hoep this helped and brainliest please