Find the value of X When 6-3x=5x-10x+6
Answers
\(6 - 3x = 5x - 10x + 6\)
\(6 - x = - 5x + 6\)
\(6 + 5x = 6 - 3x\)
\(6 = 6 - 3x + 5x\)
\(6 = 6 + 2x\)
\(2x = 6 - 6\)
\(2x = 0\)
Product of two numbers is equal to 0 if at least one of them is 0 . Since 2 is not equal to 0 , x must be equal to 0 .
Which means :-
\(x = 0\)
Therefore , the value of x = 0.
Related Questions
Which of the following is the graph of f(x) = x2 + 3x − 4? graph of a quadratic function with a minimum at 2, negative 9 and x intercepts at negative 1 and 5 graph of a quadratic function with a minimum at 3, negative 4 and x intercepts at 1 and 5 graph of a quadratic function with a minimum at 2.5, negative 2.4 and x intercepts at 1 and 4 graph of a quadratic function with a minimum at negative 1.5, negative 6.2 and x intercepts at 1 and negative 4
Answers
Answer:
x intercepts at -4 and 1,
with a minimum at (-1.5, -6.25)
Step-by-step explanation:
(x + 4)(x - 1) = 0
x = -4, 1
min = -b/2a = -3/2(1) = x = -1.5
y = (-1.5)² + 3(-1.5) - 4 = -6.25
Answer:
graph of a quadratic function with a minimum at negative 1.5, negative 6.2 and x intercepts at 1 and negative 4
Step-by-step explanation:
The graph shows the minimum is (-1.5, -6.25) and the x-intercepts are a -4 and 1. This matches the last description.
__
The x-coordinates of the offered minima are all different, so it is sufficient to know that the axis of symmetry is the line ...
x = -b/(2a) = -3/(2(1)) = -1.5 . . . . . . . for quadratic f(x) = ax² +bx +c
This is the x-coordinate of the minimum.

A number x is at least -1 and no more than 9
What is the inequality ???
Answers
- x would have to be less than or equal to 9, but greater than or equal to -1. the symbols for the greater than or equal to is the > with a line under it (in case you didn’t know) and same with the less than or equal to
Let S(t) be the number of students enrolled in a school district in terms of the number of years, t, after 2000. Which statements regarding function S are true? Select TWO that apply. Responses S(0) = 2,000 means that there were no students in the year 2000. S(0) = 2,000 means that there were no students in the year 2000. S(10)=S(5) means that there were the same number of students in 2010 as in 2005. cap s times 10 is equal to cap s times 5 means that there were the same number of students in 2010 as in 2005. S(5)= 2,024 means that there were 2,024 students in the year 2005. S(5)= 2,024 means that there were 2,024 students in the year 2005. S(15) − S(10) = −40 means that there were 40 less students in 2010 than there were in 2015. S(15) − S(10) = −40 means that there were 40 less students in 2010 than there were in 2015. S(3)= 2,015 means that there were 3 students in the year 2015.
Answers
The statements that are true regarding function S are:
S(0) = 2,000 means that there were no students in the year 2000.S(15) − S(10) = −40 means that there were 40 less students in 2010 than there were in 2015.What is function?
In mathematics, a function is a rule or a relationship between two sets of values, which associates each element of the first set (called the domain) with a unique element of the second set (called the range). The domain and range can be any sets, including numbers, letters, or other objects.
The statements that are true regarding function S are:
S(0) = 2,000 means that there were no students in the year 2000.S(15) − S(10) = −40 means that there were 40 less students in 2010 than there were in 2015.The other statements are not necessarily true:
S(10)=S(5) does not necessarily mean that there were the same number of students in 2010 as in 2005, as there could have been fluctuations in enrollment during those years.cap s times 10 is equal to cap s times 5 is not a statement but a mathematical expression that relates the number of students in 2010 to the number of students in 2005.S(5)= 2,024 is not necessarily true, as the number of students in 2005 could have been different from 2,024.S(3)= 2,015 is not necessarily true, as the year 2015 is three years after 2000, and S(3) would correspond to the number of students in 2003, not 2015.To learn more about function visit:
https://brainly.com/question/11624077
#SPJ1
Finding angle measures given two intersecting lines

Answers
Answer:
66, 114, 114
Step-by-step explanation:
angle 3=angle 1=66
angle 2=angle 4=180- angle 3=114
A farmer goes to the market to sell a box of eggs. A clumsy horse steps on the box of eggs and breaks a lot of them. The horse’s rider offers to pay for all of the eggs in the box and asks the farmer how many eggs there were. The farmer does not remember the exact number, but when she took them out of the box two at a time, there was 1 egg left. The same thing happened when she took them out three, four, five and six eggs at a time, but when she took them out 7 at a time, there were no eggs left
Answers
The smallest number of eggs that could have been in the box is 1134
The problem is to find the smallest number of eggs that could have been in the box, given the remainder when taking them out by different numbers. Here are the moves toward tackling it:
Allow n to be the quantity of eggs in the container. Then we have the accompanying arrangement of congruences:
n ≡ 1 (mod 2)
n ≡ 1 (mod 3)
n ≡ 1 (mod 4)
n ≡ 1 (mod 5)
n ≡ 1 (mod 6)
n ≡ 0 (mod 7)
For this problem, we have k = 6 k = 6, a i = {1,1,1,1,1,0} a_i = {1,1,1,1,1,0}, M i = {1260,840,630,504,420,720} M_i = {1260,840,630,504,420,720}, and y i = {−1,−2,−3,-4,-5,-6} y_i = {-1,-2,-3,-4,-5,-6}.
Plugging these values into the formula and simplifying modulo 5040, we get:
n = (−1260 + −1680 + −1890 + −2016 + −2100 + 0) mod 5040
n = (−8946) mod 5040
n = (−3906) mod 5040
n = 1134 mod 5040
Therefore, the smallest number of eggs that could have been in the box is 1134
to know more about congruences click here:
https://brainly.com/question/30818154
#SPJ4
The bottom of a cylindrical container has an area of 10 cm2 . The container is filled to a height whose mean is 5cm, and whose standard deviation is 0.1 cm. Let V denote the volume of fluid in the container.
Answers
The volume of the shape will be 50cm3.
How to calculate the volume?It should be noted that the volume van be found by multiplying the area by the height. The volume will be:
= 10 × 5
= 50cm³
The standard deviation volume will be:
= 0.1 × 50
= 5cm
Learn more about volume on:
brainly.com/question/14880458
#SPJ1
i ask for your help please help my brainly.
A dance team plans to make and sell caramel and cheddar popcorn for a fundraiser. To maximize the profit, the team captain created the feasible region below based on constraints due to the resources the team had available.
Let x represent the number of caramel popcorn bags and let y represent the number of cheddar popcorn bags. The dance team will earn a profit of $1.00 for every caramel popcorn bag they sell and $2.50 for every cheddar popcorn bag they sell.
there is 2 attachment
the vertices of the feasible region are
(____,_____) (____,_____) (____,_____) (____,_____) (____,_____)


Answers
The vertices of the feasible region are (140, 60) (120, 100) (60, 100) (40, 80) (60, 60).
As given, a dance team plans to make and sell caramel and cheddar popcorn for a fundraiser.
To maximize the profit, the team captain created the feasible region below based on constraints due to the resources
the team had available.
Let x represent the number of caramel popcorn bags and let y represent the number of cheddar popcorn bags.
The dance team will earn a profit of 1.00 for every caramel popcorn bag they sell and 2.50 for every cheddar
popcorn bag they sell.
Given:
The dance team will earn a profit of 1.00 for every caramel popcorn bag they sell and $2.50 for every cheddar popcorn bag they sell.
The feasible region:
From the graph, the vertices of the feasible region are (140, 60) (120, 100) (60, 100) (40, 80) (60, 60).
Therefore, the answer is (140, 60) (120, 100) (60, 100) (40, 80) (60, 60).
for such more question on feasible region
https://brainly.com/question/11420075
#SPJ11
Help me with this, it’s due in a bit!

Answers
Answer:
64 square centimeters
Step-by-step explanation:
The surface are of a pyramid is found by finding the sum of the area of the four sides and the base.
Finding the triangular face:
Area of triangle = \(\frac{1}{2} b h\) = \(\frac{1}{2}*4*6 = 12\)
12 * 4 (4 sides) = 48 square cm
Finding the Base = \(w * l = 4 * 4 = 16\)
Finally, we add it together. 48 + 16 = 64
What is the length of R'A'?
1.5 cm
1.6 cm
3.0 cm
3.2 cm
Answers
Answer:
1.5cm
Step-by-step explanation:
I TOOK THE TEST
which equation represents the graph of a circle
y=x^2
x^2+y^2=9
x=4
y=x
Answers
An equation that represents the graph of a circle include the following:
What is the equation of a circle?In Geometry, the standard form of the equation of a circle is modeled by this mathematical equation;
(x - h)² + (y - k)² = r²
Where:
h and k represent the coordinates at the center of a circle.r represent the radius of a circle.From the information provided above, we have the following equation of a circle has the only correct answer option:
x² + y² = 9
x² + y² = 3²
Therefore, the center (h, k) is (0, 0) and the radius is equal to 3 units.
Also, we can determine the diameter of this circle;
Diameter = 2r
Diameter = 2(3)
Diameter = 6 units.
Read more on equation of a circle here: brainly.com/question/15626679
#SPJ1
divide 100,000 by 10 scores
Answers
10)100000(10000
10
___
××0000
Answer:
5000
Step-by-step explanation:
1 score = 20
10 scores
= 10 x 20
= 200
100,000 / 10 scores
= 100,000 / 200
= 5000
in how many ways can five distinct martians and eight distinct jovians be seated at a circular table if no two martians sit together.
Answers
The number of ways to seat five distinct martians and eight distinct jovians at a circular table if no two martians sit together are :
5,644,800
To solve this problem, we can use the principle of inclusion-exclusion. First, we'll consider the number of ways to seat the eight jovians without any restrictions. This can be done in 8! ways.
Next, we'll consider the number of ways to seat the five martians if they are treated as indistinguishable. This can be done in (8+1) choose 5 ways (using stars and bars method).
However, this counts arrangements where two or more martians sit together. To account for this, we'll subtract the arrangements where two martians sit together. There are 5 ways to choose which two martians sit together, and we can treat them as a single "block" when seating the remaining three martians and eight jovians. This can be done in 7! ways.
But we've now subtracted too much, since arrangements where three martians sit together have been subtracted twice. There are 5 ways to choose which three martians sit together, and we can treat them as a single "block" when seating the remaining two martians and eight jovians. This can be done in 6! ways.
Finally, we need to add back in the arrangements where four or five martians sit together. However, since no two martians can sit together, there are no such arrangements, so we don't need to add anything back in.
Putting it all together, the number of ways to seat five distinct martians and eight distinct jovians at a circular table if no two martians sit together is:
8! * (9 choose 5) - 5 * 7! + 5 * 6! = 5644800.
Therefore, there are 5,644,800 ways to seat the martians and jovians.
To learn more about arrangements visit : https://brainly.com/question/1427391
#SPJ11
There are 28 students in a class
13 of the students are boys
two students from the class are chosen at random
if the first person chosen is a boy what is the probability that the second person also chosen is also a boy
Answers
The probability that the second person chosen will also be a boy is roughly 0.872, or 87.2%.
Since the first person chosen is a boy, there are now 12 boys and 15 girls left in the class. We want to find the probability that the second person chosen is also a boy.
The probability of choosing a boy for the first selection is 13/28. Then, for the second selection, there are now 12 boys and 27 students left, so the probability of choosing a boy is 12/27.
Using conditional probability, we can calculate the probability that the second person chosen is also a boy given that the first person chosen is a boy:
P(Second person is a boy | First person is a boy) = P(Both are boys) / P(First person is a boy)
P(Second person is a boy | First person is a boy) = (12/27) / (13/28)
P(Second person is a boy | First person is a boy) ≈ 0.872
Therefore, the probability that the second person chosen is also a boy given that the first person chosen is a boy is approximately 0.872 or 87.2%.
To learn more about probability refer to:
brainly.com/question/30034780
#SPJ4
Eight less than a third of a number is the sum of that number and one.
Answers
Answer:
\(x = -13\frac{1}{2}\)
Step-by-step explanation:
Eight less than a third of a number is the sum of that number and one.
Let the number be x.
That is:
\(\frac{1}{3}x - 8 = x + 1\\ \\=> x - \frac{1}{3}x = -8 - 1 \\\\\frac{2}{3}x = -9\\\\x = -9 * \frac{3}{2}\\ \\x = \frac{-27}{2}\)
\(x = -13\frac{1}{2}\)
Set up and evaluate the integral that gives the volume of the solid formed by revolving the region about the x-axis.
y=4−x2
Answers
The integral that gives the volume of the solid formed by revolving the region about the x-axis is V = \(\int\limits^{-2}_{-2}\)π(4−x²)² dx is (8/3)π cubic units.
To find the volume of the solid formed by revolving the region about the x-axis, we can use the disk method.
First, we need to find the limits of integration. The given function y = 4 - x² intersects the x-axis at x = -2 and x = 2. So, the limits of integration will be from -2 to 2.
Next, we need to express the given function in terms of x. Solving for x, we get x = ±√(4-y).
Now, we can set up the integral for the volume using the disk method
V = π \(\int\limits^a_b\) (f(x))² dx
where f(x) = √(4-x²), and a = -2, b = 2.
V = π \(\int\limits^{-2}_{-2}\) (√(4-x²))² dx
V = π \(\int\limits^{-2}_{-2}\) (4-x²) dx
V = π [4x - (1/3)x³] \(|^{-2}_2\)
V = π [(32/3)-(8/3)]
V = (8/3)π
Therefore, the volume of the solid formed by revolving the region about the x-axis is (8/3)π cubic units.
To know more about volume:
https://brainly.com/question/30464647
#SPJ4
What's the length of the hypotenuse of right ΔDEF shown?
Question 13 options:
A)
√87
B)
12
C)
15
D)
√117

Answers
Answer: √177
Step-by-step explanation:
6²+9²=c²
36+81=c²
117=c²
√117=√c²
√177 = c
(√177 can also be watered down to ±3√13 but √177 is one of the answer choices so yeah)
help me out, thank you !

Answers
Explanation: a ^2 +b^2 = c^2
7^2 + 10.2^2 = c^2
49 + 104.04=c^2
153.04 =c^2
c ≈ 12.37
Round: 12.4
Someone help me please!

Answers
Answer:
A: the scale is missing
i hope this helps
Step-by-step explanation:
Answer:
the numbers are supposed to start at zero and the scale is missing
what does the value of the sample correlation coefficient indicate about the relationship between the admit rate () and the -yr grad. rate ()?
Answers
The sample correlation coefficient, is represented as r, measures the strength of correlation and direction of the linear relationship between two variables. It ranges from -1 to 1. The closer the coefficient is to -1, the stronger the negative correlation, the closer it is to 1, the stronger makes the positive correlation reach towards its closer and the closer towards to the expectancy to 0, the weaker the correlation.
The correlation coefficient does not indicate the cause and effect relationship between the variables, just the association between them.
A positive correlation tells us that as one variable increases with respective its the other variable also increases, and a negative correlation means that as one variable increases with respective to its the other variable decreases.
So, the value of the sample correlation coefficient between the rates of admit and the -yr grad rate . rate can indicate if these variables are positively or negatively done as correlated and how strong is this correlation occurs.
To know more about correlation coefficient, , click here:
brainly.com/question/15577278
#SPJ4
Help me out with this question (geometry)
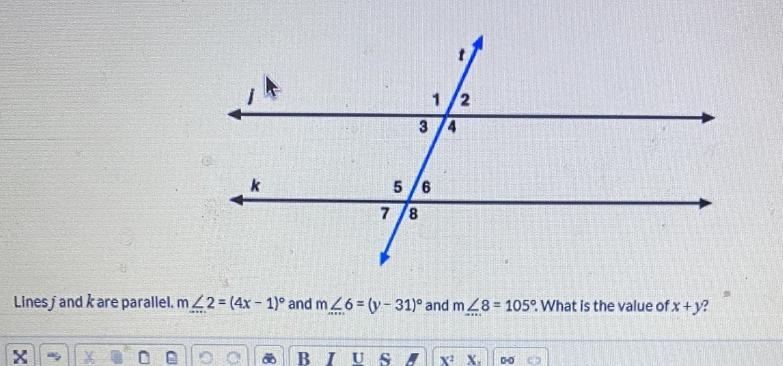
Answers
Answer:
m<8=m<4=105
m<4=180-(4x-1)
=180-4x+1
105 =-4x+181
4x= 181-105
4x=76
X=19
m<6=180-105
=75
y-31=75
y =75+31
y=106
X+y=19+106
=125
2. Write down a number that has a value less than |14.7|
Answers
Absolute Value of 14.7 is 14.7 any number below 14.7.
the number of subsets of the set of the 12 months of the year that have less than 11 elements isa. 2^12 - 13b. 2^12c, 2^12 - 1d. 2611
Answers
The number of subsets of the set of the 12 months of the year that have less than 11 elements is 2^12 - 13 (option a).
Explanation:
We want to determine the number of subsets of the set of 12 months of the year that have less than 11 elements.
1. Total number of subsets:
For any given set with n elements, the total number of subsets is 2^n. In this case, we have 12 months, so the total number of subsets is 2^12.
2. Subsets with 11 elements:
To find the number of subsets that have 11 elements, we need to choose 11 elements out of the 12 available months. This can be calculated using the combination formula:
12C11 = 12! / (11! * (12-11)!) = 12
Therefore, there are 12 subsets that have exactly 11 elements.
3. Subsets with 12 elements:
To find the number of subsets that have all 12 elements, there is only one such subset, which is the entire set of 12 months.
4. Subsets with less than 11 elements:
To determine the number of subsets with less than 11 elements, we need to subtract the subsets with 11 and 12 elements from the total number of subsets.
5. Total number of subsets - Number of subsets with 11 elements - Number of subsets with 12 elements:
2^12 - 12 - 1 = 2^12 - 13.
6. Simplifying the expression:
2^12 is equal to 4096, so the final answer is:
4096 - 13 = 4083.
Therefore, the correct answer is (a) 2^12 - 13, which represents the number of subsets of the set of 12 months of the year that have less than 11 elements.
Know more about the combination formula click here:
https://brainly.com/question/29047695
#SPJ11
OFFERING 88 POINTS AND BRAINLIEST TO THE FIRST ANSWER PLEASE HELP ME FAST

Answers
Answer
\(168in^{2}\)
Step-by-step explanation:
SA=2(wl+hl+hw)
2·(6·2+9·2+9·6)
=168
Construct a 90% confidence interval for (p 1 −p 2 ) in each of the following situations. a. n 1 =400; p^1 =0.67;n 2=400; p^ 2 =0.56. b. n 1=180; p^1=0.28;n =250;p^2=0.26. c. n 1 =100; p^1 =0.47;n 2 =120; p^2 =0.59. a. The 90% confidence interval for (p 1 −p 2 ) is (Round to the nearest thousandth as needed.)
Answers
The 90% confidence interval for (p1 - p2) in situation (a) is approximately (0.077, 0.143).
To construct a 90% confidence interval for (p1 - p2) in each of the given situations, we can use the following formula:
CI = (p1 - p2) ± Z * √((Y1 * (1 - Y1) / n1) + (Y2 * (1 - Y2) / n2))
Where:
CI = Confidence Interval
Z = Z-score corresponding to the desired confidence level (90% confidence level corresponds to Z ≈ 1.645)
Y1 = Sample proportion for group 1
Y2 = Sample proportion for group 2
n1 = Sample size for group 1
n2 = Sample size for group 2
(a) For n1 = 400, Y1 = 0.67, n2 = 400, Y2 = 0.56:
CI = (0.67 - 0.56) ± 1.645 * √((0.67 * (1 - 0.67) / 400) + (0.56 * (1 - 0.56) / 400))
CI = 0.11 ± 1.645 * √(0.00020125 + 0.000196)
CI ≈ 0.11 ± 1.645 * √0.00039725
CI ≈ 0.11 ± 1.645 * 0.0199328
CI ≈ 0.11 ± 0.0327818
CI ≈ (0.077, 0.143)
Therefore, the 90% confidence interval for (p1 - p2) in situation (a) is approximately (0.077, 0.143).
To learn more about proportion visit;
https://brainly.com/question/31548894
#SPJ11
guys FAST I ONLY HAVE 10MINS Raquel estimated 304,900,000,000 as 3 × 108. What error did she make?
Answers
Answer:
The 108 it should be more
Step-by-step explanation:
Answer:she forgot the decimal
Step-by-step explanation
In a 36% sale, the price of a phone reduced by $135.
Find the original price of the phone.
Answers
Answer:
$210.94
Step-by-step explanation:
Can I have brainliest? It would help me out, if not thanks anyways! Hope this helped and have a nice day :)
Answer:
The original price was $375.
Step-by-step explanation:
The original price of the phone is x.
36% of x is $135.
0.36x = 135
x = 135/0.36
x = 375
Answer: The original price was $375.
Lila has gained a lot of weight recently she works out and watches her intake but she's still gaining weight when she visited the doctor she told her that she had a problem with one of her endocrine glands which gland would most likely have a tissue with maintaining the breakdown of foods
Answers
Answer:
The Pancreatic gland is the gland responsible for maintaining the breakdown of foods in the body.
Step-by-step explanation:
The pancreatic gland can function as an endocrine gland, which is responsible for the secretion of glucagon and insulin. These two enzymes are responsible for the maintaining of the glucose levels of the body.
The insulin in Lila's body is meant to reduce her blood sugar, by helping the cells to be able to absorb the glucose, and use it as energy to drive her exercise and her daily routines. However, if there is a problem with the pancreas, the glucose will just be in the blood stream, without getting to the cells and Lila will keep on feeling hungry all the time. This is probably why she will keep on gaining weight.
Answer:
A. The thyroid
Step-by-step explanation:
Searched it up...
Find the area of the following shape. Show all work

Answers
Best way to solve this is by using
\( \sqrt{s(s - a)(s - b)(s - c)} \)
\(where \: s = \frac{a + b + c}{2} \)
s=(12+8+17)/2
=18.5
using the formulae
area =43.5
Twice a number x is equal to 58
How can you write this in number form?
Thank you
Answers
Answer:
Something like:
2x = 58
Hopefully that's what you're talking about.
Answer:
2x = 58 [x = 29]
Step-by-step explanation:
Twice a number x is equal to 58 implies that 2 times x is 58 which means that the expression x with a coefficient of 2 is equal to a constant of 58.
2 × x = 58 → 2x = 58
_____________________
If you want the working x value for this equation, just divide both sides by 2.
2x = 58
÷2 ÷2
______
x = 29
Factor 360 t+ 10 t^ 3- 120t^2 .
Answers
Answer:
\(10t(t-6)^2\)
Step-by-step explanation:
By looking at the equation
\(360 t+ 10 t^ 3- 120t^2\)
we can rearrange it from highest order to lowest:
\(10 t^ 3- 120t^2 +360 t\)
Now, what variable is present in all the numbers? "t" is
And what number are all the numbers divisible by? 10.
So then we can factor out a 10t from all numbers:
\(10t(t^2-12t+36)\)
Now we can factor the expression inside the brackets separately:
\(1*1=1\\(-6)*(-6)=36\)
cross these numbers to get -6 and -6, then when you add, you get -12 which is the b value.
\(10t [(t-6)(t-6)]\)
Since they're both the same:
\(10t(t-6)^2\)
:) hope this helped!