Answers
Related Questions
find the slope of the line through each pair of points (6, 10) , (-1, 10)
Answers
Answer:
-7Step-by-step explanation:
Slope is rise/run or change in y over change in x.
To calculate rise we subtract y2 from y1.
-1 - 6 = -7
RUN: -7
To calculate run we subtract x2 from x1.
10 - 10 = 0
RISE: 0
Slope is -7/0
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
Simplify the following expression.
(5h – 3)(5h – 3)

Answers
Answer: -30h +9
Step-by-step explanation:
Answer:
25h²-30h+9
Step-by-step explanation:
we need to multiply binomials
to multiply binomials using the FOIL method, we first multiply the First terms (F for first) together (in this case, 5h and 5h)
That gives us 25h²
Next up, we do the Outer terms (O for outer), which in this case are 5h and -3. This gives us -15h
then, we do the two Inner terms, (I for inner) which are -3 and 5h. This gives us -15h
finally, we do the two Last terms (L for last), which are -3 and -3. This gives us 9
here's what we have from doing FOIL:
25h²-15h-15h+9
we can combine the 2 -15h's together to get:
25h²-30h+9
Hope this helps!
Is it cheaper to buy 10 single apples or buy them in a bundle of 10?
Plz help I’m not trying to fail
Answers
it's easy to by them Cheaper tbh with you
and it's a quiz Right??
Answer:
A bundle always cheaper than a single apple.
Step-by-step explanation:
Bundling helps to increase efficiencies and reduce marketing and distribution as well as maintenance cost.
A class consists of 12 boys and 10 girls. How many ways can a committee of 9 be chosen if: a. There are no further restrictions? b. The principal's daughter must be on the committee? The twins Larry (boy) and Mary (girl) cannot both be on the committee? d. There must be at least one boy and one girl on the committee?
Answers
a. There are approximately 21,175,560 ways to choose a committee of 9 with no further restrictions.
b. There are 2,716 ways to choose a committee of 9 with the principal's daughter on the committee.
c. There are 21,153,128 ways to choose a committee of 9 where the twins Larry and Mary cannot both be on the committee.
d. There are 21,175,330 ways to choose a committee of 9 with at least one boy and one girl.
a. The number of ways to choose a committee of 9 with no further restrictions:
To calculate the number of ways to choose a committee of 9 without any restrictions, we can use the combination formula.
The total number of students in the class is 12 boys + 10 girls = 22 students.
The number of ways to choose a committee of 9 from 22 students is given by the combination formula:
C(n, r) = n! / (r!(n - r)!)
Where n is the total number of students (22) and r is the number of students to be chosen (9).
Using the formula, we can calculate:
C(22, 9) = 22! / (9!(22 - 9)!)
= 22! / (9! * 13!)
≈ 21,175,560
here are approximately 21,175,560 ways to choose a committee of 9 with no further restrictions.
b. The number of ways to choose a committee of 9 where the principal's daughter must be on the committee:
Since the principal's daughter must be on the committee, we only need to choose the remaining 8 members from the remaining 21 students (excluding the principal's daughter).
The number of ways to choose 8 students from 21 is given by the combination formula:
C(21, 8) = 21! / (8!(21 - 8)!)
= 21! / (8! * 13!)
= 2,716
There are 2,716 ways to choose a committee of 9 where the principal's daughter must be on the committee.
c. The number of ways to choose a committee of 9 where the twins Larry (boy) and Mary (girl) cannot both be on the committee:
To calculate the number of ways to choose a committee of 9 where the twins Larry and Mary cannot both be on the committee, we need to subtract the number of cases where they are both on the committee from the total number of ways without any restrictions.
First, calculate the number of ways to choose a committee of 9 without any restrictions (as calculated in part a):
Total ways = 21,175,560
Next, calculate the number of ways where both Larry and Mary are on the committee. Since they cannot both be on the committee, we treat them as a single entity and choose the remaining 7 members from the remaining 20 students (excluding Larry, Mary, and the principal's daughter):
C(20, 7) = 20! / (7!(20 - 7)!)
= 20! / (7! * 13!)
= 77520
Subtracting the number of ways where Larry and Mary are both on the committee from the total ways, we get:
Total ways - Ways with Larry and Mary = 21,175,560 - 77,520
= 21,153,128
There are 21,153,128 ways to choose a committee of 9 where the twins Larry and Mary cannot both be on the committee.
d. The number of ways to choose a committee of 9 with at least one boy and one girl:
To calculate the number of ways to choose a committee of 9 with at least one boy and one girl, we need to subtract the cases where there are only boys or only girls from the total number of ways without any restrictions.
First, calculate the total number of ways to choose a committee of 9 without any restrictions (as calculated in part a):
Total ways = 21,175,560
Next, calculate the number of ways to choose a committee with only boys. We can choose 9 boys from the 12 available boys:
C(12, 9) = 12! / (9!(12 - 9)!)
= 12! / (9! * 3!)
= 220
Similarly, calculate the number of ways to choose a committee with only girls. We can choose 9 girls from the 10 available girls:
C(10, 9) = 10! / (9!(10 - 9)!)
= 10! / (9! * 1!)
= 10
Subtracting the cases with only boys and only girls from the total ways, we get:
Total ways - Ways with only boys - Ways with only girls = 21,175,560 - 220 - 10
= 21,175,560 - 230
= 21,175,330
There are 21,175,330 ways to choose a committee of 9 with at least one boy and one girl.
To know more about restrictions, visit
https://brainly.com/question/30195877
#SPJ11
Find the solution of the system of equations.
-x+2y=-15
8x-2y=-20
Answers
Answer:
the answer is (-5,-10)
hope this helps :)
simplify x(2x+1)-(4x-5)
Answers
WAIT I THINK X = 3±i√31/4
Answer:
2x*-3x-5
* = squared
Step-by-step explanation:
step 1: distribute “x” to “2x+1”
-you now have the equation: 2x*+1x-4x-5
step 2: combine like terms (combine “1x” and “-4x”. that gets you “-3x”.)
-you now have the equation: 2x*-3x-5
step 3: you have no more like terms, your equation is solved.
final equation: 2x*-3x-5
I forgot how to do these, and i don’t remember whether they have two answers or not.
Solve for d.
-7| d - 1 | = -11
Answers
Answer:
=18/7
=−4/7
Step-by-step explanation:
Divide both sides by -7
−7|−1|=−11
The negatives are canceled.
Simplify
|−1|=11/7
Split the problem into two cases: one positive and one negative
=18/7
=−4/7
NEED HELP ASAP
...is g0d real? I need honest answers please explain why or why not.
Answers
If A is a 9x6 matrix, what is the largest possible dimension of the row space of A? If A is a 6x9 matrix, what is the largest possible dimension of the row space of A? Explain.
Answers
If A has rank 6, then it has 6 linearly independent rows and its row space has dimension 6. If the rank of A is less than 6, then the dimension of the row space will be less than 6.
The row space of a matrix is the span of its row vectors. Therefore, the dimension of the row space is equal to the number of linearly independent rows of the matrix.
For a 9x6 matrix A, the largest possible dimension of the row space is 6. This is because there can be at most 6 linearly independent rows in a 9x6 matrix. If there were more than 6 linearly independent rows, then the matrix would have rank greater than 6, which is impossible since the maximum rank of a 9x6 matrix is 6.
For a 6x9 matrix A, the largest possible dimension of the row space is also 6. This is because the number of linearly independent rows cannot exceed the number of columns in the matrix.
Therefore, if A has rank 6, then it has 6 linearly independent rows and its row space has dimension 6.
However, if the rank of A is less than 6, then the dimension of the row space will be less than 6.
Know more about the linearly independent rows
https://brainly.com/question/31086895
#SPJ11
An athletic facility is building an indoor track. The track is composed of a rectangle and two semicircles.
a. Write a formula for the perimeter of the indoor track
P=
b. Solve the formula for x.
x=
c. The perimeter of the track is 660 feet, and r is 50 feet. Find x. Round to the nearest foot.
x=____feet
Answers
Answer:
(The image is not provided, so i draw an idea of how i supposed that the problem is, the image is at the bottom)
Ok, we have a rectangle of length x by r.
At the extremes of length r, we add two semicircles.
So the perimeter will be equal to:
Two times x, plus the perimeter of the two semicircles (that can be thought as only one circle).
The radius of the semicircles is r, and the perimeter of a circle is:
C = 2*pi*r
where pi = 3.14
Then the perimeter of the track is:
P = 2*x + 2*pi*r.
b) now we want to solve this for x, this means isolating x in one side of the equation.
P - 2*pi*r = 2*x
P/2 - pi*r = x.
c) now we have:
P = 660ft
r = 50ft
then we can replace the values and find x.
x = 660ft/2 - 3.14*50ft = 173ft

A local repair shop charges $109 per hour to fix cars. A new water pump costs $249. 98. How many hours does the mechanic work, if the total cost of installing a new water pump is $849. 48?
Answers
The mechanic worked for 5.5 hours to install the new water pump.
Let's assume the mechanic worked for "x" hours to install the water pump.
The cost of the repair work will include the cost of the water pump as well as the labor charges.
The cost of the water pump is given as $249.98.
The labor charges can be calculated by multiplying the hourly rate by the number of hours worked.
So, the labor charges will be $109 multiplied by "x" hours, which is $109x.
Adding the cost of the water pump to the labor charges will give us the total cost of the repair work.
Therefore, we can write the equation as:
$849.48 = $109x + $249.98
Simplifying the equation, we get:
$599.50 = $109x
Dividing both sides by $109, we get:
x = 5.5
Therefore, the mechanic worked for 5.5 hours to install the new water pump.
To know more about the surface area here
https://brainly.com/question/16519513
#SPJ4
Sundaybought10pens,andapencost$5dollars.whatisthecostof15pensinnaira,if$1is30naira?
Answers
The cost of 15 pens in INR, considering the given exchange rate, is 2250 INR which is obtained by using arithmetic operations.
Sunday bought 10 pens at a cost of $5 each. To find the cost of 15 pens in INR, considering the exchange rate of $1 being equal to 30 INR, the total cost can be calculated by multiplying the cost per pen by the number of pens and then converting it to INR.
The cost of a single pen is given as $5. To calculate the cost of 15 pens, we can multiply the cost per pen by the number of pens:
Cost of 15 pens = Cost per pen * Number of pens
Cost of 15 pens = $5 * 15 = $75
To convert the cost from dollars to INR, we use the given exchange rate of $1 being equal to 30 INR. Thus, we can multiply the cost in dollars by the conversion rate:
Cost in INR = Cost in dollars * Conversion rate
Cost in INR = $75 * 30 = 2250 INR
Therefore, the cost of 15 pens is 2250 INR.
Learn more about arithmetic operations here:
https://brainly.com/question/30553381
#SPJ11
The complete question is:
Sunday bought 10 pens, and a pen cost $5 dollars. What is the cost of 15 pens in INR, if $1 is 30 INR?
Find the volume of a cone with radius 10 feet and height of 4 feet.
Answers
Answer:
\(\frac{400}{3} \pi\)
Step-by-step explanation:
Formula for Cone: π\(r^{2}\frac{h}{3}\)
Since we have all the components, we can find the volume of the cone.
R = 10
H = 4
π\(10^{2}\frac{4}{3}\)
10×10 = 100
100π\(}\frac{4}{3}\)
\(}\frac{4}{3}\)×100
4 100 400
--- × ----- = ------
3 1 3
Answer: \(\frac{400}{3} \pi\)
Hope this helped.
Find the volume of a cone with radius 10 feet and height of 4 feet.
Solution :Given Data :
Radius = 10 feet
Height = 4 feet
Formulae :
\( \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \star \: \blue{ \underline{ \overline{ \green{ \boxed{ \frak{{ \sf V}olume_{(Cone)} = \pi {r}^{2} \frac{h}{3}}}}}}}\)
Putting the values we get
\( \frak{ Volume_{(Cone)} = 3.14 × (10)² × \frac{4}{3} }\)
\( \frak{Volume_{(Cone)} = 3.14 × 100 × \frac{4}{3} }\)
\( \frak{Volume_{(Cone)} = 314 \times \frac{4}{3} }\)
\( \frak{Volume_{(Cone)} = 418.67 \: ft³ }\)
Henceforth, the volume is 418.67 ft³
Express a^-6 with a positive exponent
Answers
Answer:
\(\frac{1}{a^{6} }\)
Step-by-step explanation:
using the rule of exponents
\(a^{-m}\) = \(\frac{1}{a^{m} }\) , then
\(a^{-6}\) = \(\frac{1}{a^{6} }\)
pleas help please helpppp

Answers
Answer:
the third option
Step-by-step explanation:
the inverse of a statement is just the opposite. So the opposite of your statement would be "if a quadrilateral is NOT a rectangle, then it is NOT a parallelogram."
hope this helps!
5) The teacher distributes 4 pencils per student. Can you tell how many pencils are needed for given number of students? (Use s for the number of students.)
Answers
Answer:
Step-by-step explanation:
The number of pencils distributed per student is 5.
Let the given number of students be
Total number of pencils needed = Number of pencils distributed per student × Number of studentsTotal number of pencils needed = 5 × s = 5s.
HELP MEEE PLEASEE SHOOW UR WOORRKK

Answers
Answer:
b
Step-by-step explanation:
2(k-5)+3k=k+6
step 1 distribute the 2 to whats in the parenthesis
2k-10+3k=k+6
step 2 combine any like terms if there are any
5k-10=k+6
step 3 add 10 to each side
5k=k+16
step 4 subtract 1k from each side
4k=16
step 5 divide each side by 4
k=4
In the diagram below, triangle ABC is congruent to triangle DEF.
A
4 cm
85°
6 cm
60°
35
С
7 cm
B
Which two angles are corresponding?
А
ZA and ZE
B
ZB and D
c
ZA and F
D
ZC and F

Answers
Answer:
D. ∠C and ∠FStep-by-step explanation:
Triangle DEF is triangle ABC rotated by 180°
So:
∠A is corresponding to ∠D
∠B is corresponding to ∠B
and ∠C is corresponding to ∠F
Bao buys a skateboard that originally cost $38. He uses a coupon to save 20%. How many dollars does Bao pay for the skateboard?
Answers
Answer:
$30.40
Step-by-step explanation:
Barty is going to flip a coin three times. What is the probability that he will see at least
two tails? Can you use a Probability Area Model for this situation?
Answers
Answer:
1/2
Step-by-step explanation:
For three coin tosses, the posible outcomes are:
[(HHH), (HHT), ( THH), (HTH), ( THT), (TTH), (HTT), (TTT)
The outcomes where there are at least 2 tails are:
(TTT), (TTH), (THT), (HTT)
So, the probability that the coin will land tails at least 2 times is 4/8 or 1/2
You measure the lifetime of a random sample of 25 rats that are exposed to 10Sv of radiation (the equivalent of 1000 REM) for with the LD100 is 14 days. The sample mean is x=13.8 days. Suppose that the lifetimes for this level of exposure follow a normal distribution with unknown mean and standard deviation 0.75. you read a report that says "on the basis of random sample of 25 rats, a confidence interval for the true mean survival time extends from 13.45 to 14.15 days." The confidence level for this interval is?
Answers
The confidence level for the given interval of 13.45 to 14.15 days is 95%, which means that we can be 95% confident that the true mean survival time falls within this range.
Based on the given information, we know that a random sample of 25 rats exposed to 10Sv of radiation has a mean lifetime of x=13.8 days. We also know that the LD100 is 14 days, and that the lifetimes for this level of exposure follow a normal distribution with unknown mean and standard deviation 0.75.
The report states that a confidence interval for the true mean survival time extends from 13.45 to 14.15 days, which means that we can be 95% confident that the true mean survival time falls within this range. This is because the confidence level for this interval is 95%.
To calculate this, we can use the formula:
Confidence level = 1 - alpha
where alpha is the significance level, which is typically set to 0.05 for a 95% confidence level. This means that there is a 5% chance that the true mean survival time is outside the given interval.
In conclusion, the confidence level for the given interval of 13.45 to 14.15 days is 95%, which means that we can be 95% confident that the true mean survival time falls within this range.
Learn more about confidence here:
https://brainly.com/question/15869639
#SPJ11
1. The heights of American adult males are normally distributed with a mean of 177 cm and a standard deviation of 7.4 cm. Use the Empirical Rule to find the range of heights that contain approximately(a) 68% of the data cm -- cm(b) 95% of the data cm -- cm(c) 99.7% of the data cm -- cm

Answers
what is 44/9 as a decimal and if there is a repeating number in its division just put it.
Answers
Answer:
What is 44/9 as a decimal? 4.88 (8 is repeating)

Use the law of sines to find the value of y. Round to the nearest tenth.
Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction
1.4 units
1.6 units
2.5 units
2.6 units
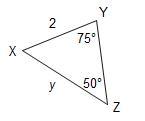
Answers
Answer:
b) 1.6 units
y = 1.586 ≅ 1.6 units
Step-by-step explanation:
Explanation:-
step(i):-
The sine rule
\(\frac{a}{Sin A} = \frac{b}{Sin B} = \frac{c}{Sin C} = 2 R\)
Given a = 2 and b = y
∠A = 75° and ∠ B = 50°
Step(ii):-
by sine rule
\(\frac{a}{Sin A} = \frac{b}{Sin B}\)
\(\frac{2}{Sin 75} = \frac{y}{Sin 50}\)
Cross multiplication , we get
2 × sin 50° = y sin 75°
2 × 0.766 = y × 0.9659
\(y = \frac{ 2 X 0.766}{0.9659} = 1. 586\)
y = 1.586 ≅ 1.6 units
Answer:
Step-by-step explanation:

negative six subtracted from the quotient of negative seventy -two and nine
Answers
The expression "negative six subtracted from the quotient of negative seventy-two and nine" can be written as:
(-72 / 9) - 6
The quotient of -72 and 9 is -8, so the expression simplifies to:
-8 - 6 = -14
Therefore, the answer is -14.
A film show lasted for 3 3/2 hours. Out of this ,1 1/3 hours were spent on advertisements. What was the actual duration of the film
Answers
3 3/2 hours as a decimal= 4.5
1 1/3 hours as a decimal = 1.3
Duration of the film show = 4.5 hours
Hours spent on advertisements = 1.3 hours
Actual duration of the film = 4.5 - 1.3 hours
= 3.2 hours
3.2 hours as a fraction = 3 1/5 hours.
Therefore, the actual duration of the film was 3 1/5 hours.
Movie lasted 3 hours and 10 minutes
You have to convert 3 3/2 and 1 1/3 to a fraction.You have to multiply 9/2 by 3 and 4/3 by 2 to get the least common multiple of those two numbers.Subtract 8/6 from 27/6 and you get 19/6.Convert 19/6 into a mixed number and you get 3 1/6 which is 3 hours and 10 minutes because the clock has 60 minutes so 1/6 is ten minutes.\(3\frac{3}{2} - 1 \frac{1}{3} = \frac{9}{2} - \frac{4}{3} = \frac{27 - 8}{6} = \frac{19}{6} = 3 \: \frac{1}{6} \)
4. A quadrilateral but no equal sides and angles is called _______.
help

Answers
\( \boxed{ \frak{Answer}}\)
Trapezium\( \sf \blue{explanation}\)
Trapezium is a quadrilateral which sides and angles are not equal.
\( \boxed{ \frak{Keep \: Learning}}\)
\( \frak{Be \: Brainly}\)
Answer:
Trapezium
#carry on learning
PLEASE HELPP SORRY ABT THE WRITING

Answers
Using relevant theorems the measures are:
1. x = 61°; y = 61° 2. x = 12; y = 7 3. x = 5; y = 13
4. x = 97°; 5. x = 6 6. x = 9
How to Find the Values of x and y Using Theorems?1. x = 61° [based on the vertical angles theorem]
y = 61° [based on the corresponding angles theorem]
2. 8x = 96 [based on the corresponding angles theorem]
x = 96/8
x = 12
8x = 11y + 19 [based on the vertical angles theorem]
Plug in the value of x:
8(12) = 11y + 19
96 = 11y + 19
96 - 19 = 11y
77 = 11y
77/11 = y
y = 7
3. 8x + 2 = 42 [based on the alternate interior angles theorem]
8x = 42 - 2
8x = 40
x = 40/8
x = 5
8x + 2 + [6(2y - 3)] = 180 [based on the linear angles theorem]
8(5) + 2 + 12y - 18 = 180
40 + 12y - 16 = 180
24 + 12y = 180
12y = 180 - 24
12y = 156
y = 156/12
y = 13
4. x = 97° [corresponding angles theorem]
5. 8x = 4x + 24 [based on the alternate exterior angles theorem]
8x - 4x = 24
4x = 24
x = 6
6. 11x + 33 + 6x - 6 = 180
17x + 27 = 180
17x = 180 - 27
17x = 153
x = 9
Learn more about theorems on:
https://brainly.com/question/11280470
#SPJ1
(a) The mean life span of a tire is 80467 kilometers. Assume that the life span of tires is normally distributed and the population standard deviation is 1287 kilometers. If a sample of 100 tires is selected randomly, compute probability that their mean life span is more than 80789 kilometers. (b) A sample of 100 factory workers found the average overtime hours works in a week is 7.8 with standard deviation 4.1 hours. (i) Find the best point estimate of the population mean. (ii) Find 90% confidence interval of the mean score for all gamers. (iii) Find 95% confidence interval of the mean score for all gamers. (iv) From your answer in part (ii) and (iii), state which sample has shorter interval.
Answers
(a). To compute the probability that the mean life span of a sample of 100 tires is more than 80789 kilometers, we can use the Central Limit Theorem and the z-score.
Given:
- Mean life span of a tire \((\(\mu\))\) = 80467 kilometers
- Population standard deviation \((\(\sigma\))\) = 1287 kilometers
- Sample size n = 100
- Desired value x = 80789 kilometers
The sample mean \((\(\bar{x}\))\) follows a normal distribution with mean \(\(\mu\)\) and standard deviation \($\(\frac{\sigma}{\sqrt{n}}\)\). Using the Central Limit Theorem, we can approximate the sample mean distribution as a normal distribution.
To calculate the z-score, we can use the formula:
\($\[ z = \frac{x - \mu}{\frac{\sigma}{\sqrt{n}}} \]\)
Substituting the given values into the formula:
\($\[ z = \frac{80789 - 80467}{\frac{1287}{\sqrt{100}}} \]\)
Calculating the expression inside the parentheses:
\($\[ \frac{1287}{\sqrt{100}} = 128.7 \]\)
Substituting the values into the z-score formula:
\($\[ z = \frac{80789 - 80467}{128.7} \]\)
\(\[ z \approx 2.518 \]\)
Using a standard normal distribution table or calculator, we can find the probability associated with a z-score of 2.518.
The probability corresponds to the area under the curve to the right of the z-score.
The probability that the mean life span of the sample of 100 tires is more than 80789 kilometers is approximately 0.0058, or 0.58%.
(b) Given:
- Sample size n = 100
- Sample mean \((\(\bar{x}\))\) = 7.8 hours
- Sample standard deviation s = 4.1 hours
(i) The best point estimate of the population mean is the sample mean itself.
Therefore, the best point estimate of the population mean is 7.8 hours.
(ii) To find the 90% confidence interval of the mean score for all gamers, we can use the t-distribution since the population standard deviation is not known.
The formula for the confidence interval for the mean is:
\($\[ \text{CI} = \bar{x} \pm t \cdot \left(\frac{s}{\sqrt{n}}\right) \]\)
where:
- \(\(\bar{x}\)\) is the sample mean (7.8 hours),
- t is the t-score corresponding to the desired confidence level (90%) and degrees of freedom (99),
- s is the sample standard deviation (4.1 hours),
- n is the sample size (100).
To find the t-score, we need to determine the degrees of freedom. For a sample size of 100, the degrees of freedom df is 100 - 1 = 99.
Looking up the t-score for a 90% confidence level and 99 degrees of freedom, we find \(\(t \approx 1.660\)\).
Substituting the given values into the confidence interval formula:
\($\[ \text{CI} = 7.8 \pm 1.660 \cdot \left(\frac{4.1}{\sqrt{100}}\right) \]\)
Calculating the expression inside the parentheses:
\($\[ \left(\frac{4.1}{\sqrt{100}}\right) = 0.41 \]\)
Substituting the values into the confidence interval formula:
\($\[ \text{CI} = 7.8 \pm 1.660 \cdot 0.41 \]\)
Calculating the interval:
\(\[ \text{CI} = (7.126, 8.474) \]\)
Therefore, the 90% confidence interval of the mean score for all gamers is approximately (7.126, 8.474) hours.
(iii) To find the 95% confidence interval of the mean score for all gamers, we can follow the same steps as in part (ii) but with a different t-score corresponding to a 95% confidence level and 99 degrees of freedom.
Looking up the t-score for a 95% confidence level and 99 degrees of freedom, we find \(\(t \approx 1.984\)\).
Substituting the given values into the confidence interval formula:
\($\[ \text{CI} = 7.8 \pm 1.984 \cdot \left(\frac{4.1}{\sqrt{100}}\right) \]\)
Calculating the expression inside the parentheses:
\($\[ \left(\frac{4.1}{\sqrt{100}}\right) = 0.41 \]\)
Substituting the values into the confidence interval formula:
\($\[ \text{CI} = 7.8 \pm 1.984 \cdot 0.41 \]\)
Calculating the interval:
\($\[ \text{CI} = (7.069, 8.531) \]\)
Therefore, the 95% confidence interval of the mean score for all gamers is approximately (7.069, 8.531) hours.
(iv) Comparing the confidence intervals from part (ii) and part (iii), we can observe that the 95% confidence interval (7.069, 8.531) has a larger interval width compared to the 90% confidence interval (7.126, 8.474). This means that the 95% confidence interval is wider and has a greater range of possible values than the 90% confidence interval.
To know more about Central Limit Theorem visit:
https://brainly.com/question/898534
#SPJ11
