The scale on a map is 3cm=15miles. Mr. Rollins measures the distance to the next at 8cm. How many miles away is the next town?
Answers
Related Questions
The sum of 7/8 of a number and 20 is 34 at minimum
Answers
Answer:
7/8x ≥ 14
Step-by-step explanation:
(sum means addition in case you forgot)
You would start by writing 7/8x + 20 ≥ 34
You would then subtract 20 from both sides to isolate the variable x.
You would then have 7/8x ≥ 14
Match each linear system with one of the phase plane direction fields.
(The blue lines are the arrow shafts, and the black dots are the arrow tips.)
I need help. I don't know how to use the eigenvalues and take that information and put it on a graph. Please explain thoroughly! Thanks.
Answers
The correct match for each linear system with one of the phase plane direction fields will be:
1:B
2:C
3:D
4:A
What is plane?
In geometry, a plane is a surface made up of all the straight lines connecting any two locations on it. It is, in other words, a level or flat surface. A plane is uniquely defined in a Euclidean space of any number of dimensions by one of the following: three non-collinear points are used. Other names for it include a two-dimensional surface. A plane has an unlimited width, an endless length, zero thickness, and no curvature. The flat surfaces of a cube or cuboid, as well as the flat surface of paper, are all true instances of geometric planes, despite the fact that it is difficult to envision a plane in real life.
To know more about plane,
brainly.com/question/2834992
#SPJ4
Match Each inequality to the number line that represents its solution

Answers
Using the order of the number lines, the correspondent inequalities that go in each box are:
x - 51 ≤ -43x - 99 ≤ - 10475 < 69 - x150 + x ≤ 144How to match the inequalities?First we need to solve each one of the inequalities, to do that, we need to isolate the variable in each one.
For the first one:
x - 99 ≤ - 104
x ≤ -104 + 99
x ≤ -5
The second one gives:
x - 51 ≤ -43
x ≤ -43 + 51
x ≤ 8
The third one gives:
150 + x ≤ 144
x ≤ 144 - 150
x ≤ -6
The last one gives:
75 < 69 - x
x < 69 - 75
x < -6
Notice that the last two are similar,the difference is that in the first one -6 is a solution, so you will see a red dot at x = -6, while in the second one- 6 is not a solution, so the circle should be white.
Then order of the inequalities from top top bottom is:
x - 51 ≤ -43
x - 99 ≤ - 104
75 < 69 - x
150 + x ≤ 144
Learn more about inequalities at:
https://brainly.com/question/25275758
#SPJ1
A calf raiser mixes a batch of milk replacer for 15 calves. Each calf gets two
quarts of milk replacer. If the calf raiser uses 960 oz. of replacer and needs to
add 34 as much water as milk replacer, how many ounces of water does she need?
Answers
Answer:
The calf raiser uses 960 oz of milk replacer for 15 calves, so each calf gets 960 oz / 15 = 64 oz of milk replacer.
To convert this to quarts, we need to divide by 32 (since there are 32 oz in a quart)
64 oz / 32 oz/quart = 2 quarts
Each calf gets 2 quarts of milk replacer and the calf raiser needs to add 34 as much water as milk replacer
So the total amount of water she needs is 2*34 = 68 quarts
To convert the quarts of water to ounces we need to multiply by 32 (since there are 32 oz in a quart)
68 quarts * 32 oz/quart = 2176 oz of water.
So the calf raiser needs 2176 ounces of water to mix with the milk replacer for 15 calves.
For question 15-16, find the value of x that would prove y || z. State the conserve used to support your answer.
Answers
Answer:
There is not enough information, but in any case, rephrase.
let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. let g be the function given by
Answers
The value of g(2) = -1/4 and the value of g(-2) is π/2 - 3/2
Consider function g(x)
\(g(x) = \int\limits^x_1 {f(t)} dt\)
Here, function f be the continuous function defined on interval [-4, 3]
The graph of function f is shown below.
It consists of three line segments and a semicircle centered at the origin, is given above.
For x = 2,
g(2)
\(=\int\limits^2_1 {f(t)} dt\)
= -(1/2) × 1 × (1/2) .........(From the graph of function f)
= -1/4
For x = -2,
g(-2)
\(=\int\limits^{-2}_1 {f(t)} dt\\\\=-\int\limits^{1}_{-2} {f(t)} dt\)
= -(3/2 - π/2) .........(From the graph of function f)
= π/2 - 3/2
Learn more about the function here:
https://brainly.com/question/28278699
#SPJ4
The complete question is:
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x) = \int\limits^x_1 {f(t)} dt\)
Frin dthe values of g(2) and g(-2)
![let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/ToaUUODoVjwiLmxJ4B9RWzroBdI3Cvr1.jpeg)
How many cyclists are at least 26 years old?
Answers
Answer:
15
Step-by-step explanation:
Assume that the situation can be expressed as a linear cost function. Find the cost function in this case.
Marginal cost: $15; 150 items cost $5500 to produce.
The linear cost function is C(x) =
Answers
The linear cost function is C(x) = 15x + 3250 and the cost function in marginal cost: $15; 150 items cost $5500 to produce is $ 5500 .
The linear operate is expressed as y = mx + b .....(1)A linear value operate expresses value as a linear operate of the amount of items;Let C(x) is that the total value, and x is that the range of things.
The slope "m" is named the cost and "b" is named the charge.
The value of m is $15 and the price of "x" is 150.
Total cost of 150 items are $5500
Substitute all the values within the equation (1) , we get
5500 = 15 (150) + b
5500 = 2250 + b
3250 = b
Hence , linear cost function is given by C(x) = 15x + 3250
Learn more about linear cost function here :
https://brainly.com/question/4025726
#SPJ9
What equation is graphed?
10
8
6
SK
-10-8-8/ 2 4 6 8 10
-8
-10
16
9
=1
=1
po

Answers
first off, let's take a peek at the picture above
hmmm the hyperbola is opening sideways, that means it has a horizontal traverse axis, it also means that the positive fraction will be the one with the "x" variable in it.
now, the length of the horizontal traverse axis is 4 units, from vertex to vertex, that means the "a" component of the hyperbola is half that or 2 units, and 2² = 4, with a center at the origin.
\(\textit{hyperbolas, horizontal traverse axis } \\\\ \cfrac{(x- h)^2}{ a^2}-\cfrac{(y- k)^2}{ b^2}=1 \qquad \begin{cases} center\ ( h, k)\\ vertices\ ( h\pm a, k)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad \sqrt{ a ^2 + b ^2} \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{(x- 0)^2}{ 2^2}-\cfrac{(y- 0)^2}{ (\sqrt{3})^2}=1\implies {\Large \begin{array}{llll} \cfrac{x^2}{4}-\cfrac{y^2}{3}=1 \end{array}}\)
A. Use a triple integral to find the volume of the given solid. The tetrahedron enclosed by the coordinate planes and the plane8x + y + z = 2B. Find the volume of the smaller wedge cut from a sphere of radius 4 by two planes that intersect along a diameter at an angle of π/6.
Answers
The volume of the smaller wedge cut from a sphere of radius 4 by two planes that intersect along a diameter at an angle of π/6 is 1/6.
What is volume ?
Volume is a measurement of three-dimensional space that is occupied. It is frequently expressed quantitatively using SI-derived units, as well as several imperial or US-standard units. Volume and the notion of length are connected.
Consider that the tetrahedron is bounded by the coordinate planes and the plane 8 x+y+z=2
Evaluate the triple integral \(\iiint_E d V$.\)
The lower boundary of tetrahedron is the plane z=0 and the upper boundary of tetrahedron is the plane z=2-8 x-y.
And the projection is y=2-8 x.
The x-limits are obtained by taking y=0 and z=0 in 8 x+y+z=2.
\($$\begin{array}{r}8 x=2 \\x=\frac{2}{8} \\x=\frac{1}{4}\end{array}$$\)
Therefore, the region becomes \($R=\left\{(x, y, z) / 0 \leq x \leq \frac{1}{4}, 0 \leq y \leq 2-8 x, 0 \leq z \leq 2-8 x-y\right\}$\).
Therefore, the integral becomes
\($ \iiint_E d V=\int_0^{\frac{1}{4}} \int_0^{2-8 x} \int_0^{2-8 x-y} d z d y d x $\)
\($=\int_0^{\frac{1}{4}} \int_0^{2-8 x}[z]_0^{2-8 x-y} d y d x $\)
\($ =\int_0^{\frac{1}{4}} \int_0^{2-8 x}[2-8 x-y] d y d x $\)
\($ =\int_0^{\frac{1}{4}}\left[2 y-8 x y-\frac{y^2}{2}\right]_0^{2-8 x} d x . $\)
\($ =\int_0^{\frac{1}{4}}\left[2(2-8 x)-8 x(2-8 x)-\frac{(2-8 x)^2}{2}\right] d x $\)
\($ =\int_0^{\frac{1}{4}}\left[32 x^2-16 x+2\right] d x $\)
\($ =\left[32\left(\frac{x^3}{3}\right)-16\left(\frac{x^2}{2}\right)+2 x\right]_0 $\)
\($ =32\left(\frac{\left(\frac{1}{4}\right)^3}{3}\right)-16\left(\frac{\left(\frac{1}{4}\right)^2}{2}\right)+2\left(\frac{1}{4}\right)-0 $\)
\($ =\frac{1}{6} $\)
To learn more about Volume visit:https://brainly.com/question/13338592
#SPJ4
PLEASE HELP FAST WILL GE T BRAINLIEST!!

Answers
Answer:
Step-by-step explanation:
bro get some lighting in ur room and set it on a table,i cant even see what im lookking at ._.
Q3. Given that the area of sector below is 85cm^2 work out its radius, marked p on the
diagram.
Give your answer correct to 1 decimal place

Answers
The radius of the circle, marked p on the diagram, is approximately 5.8 cm.
What is radius?Radius is a term used in geometry to describe the distance from the center of a circle to any point on the circumference. It is a line segment that has its two endpoints at the center of the circle and at any point on the circumference.
The area of a sector is equal to the fraction of the circle's area that the sector occupies multiplied by the area of the entire circle.
Therefore, the area of the sector is equal to (θ/360) × πr^2.
Since the area of the sector is given as 85 cm^2, we can rearrange the equation to get:
85 = (θ/360) × πr^2
Rearranging further, we get:
r^2 = (85 × 360)/(πθ)
Taking the square root of both sides, we get:
r = √((85 × 360)/(πθ))
Since the angle θ is not given, we cannot solve for r. However, we can approximate the angle θ to be equal to 360° since the sector occupies the entire circle.
Therefore, the radius of the circle is equal to:
r = √((85 × 360)/(π × 360))
r = √(85/π)
r ≈ 5.8 cm
Therefore, the radius of the circle, marked p on the diagram, is approximately 5.8 cm.
To learn more about radius
https://brainly.com/question/29614115
#SPJ1
Which diagram has all of the correct lines of reflectional symmetry for the regular pentagon? A pentagon has 3 lines of reflectional symmetry. They intersect near the bottom of the figure. A pentagon has 5 lines of reflectional symmetry. They intersect in the center of the figure. A pentagon has 1 vertical line of reflectional symmetry. A pentagon has 3 lines of reflectional symmetry that intersect in the center of the figure.
Answers
Answer:
It is B
Step-by-step explanation:
Edge 2020
Convert 10 pounds and 12 ounces to ounces.
Answers
Answer: 172 ounces
Step-by-step explanation:
We are given 10 pounds and 12 ounces to convert to ounces.
There are 16 ounces in 1 pound.
We can create a proportion to find out how much ounces 10 pounds is.
10 pounds / x ounces = 1 pound / 16 ounces
We need to solve for x by isolating the variable x.
10/x = 1/16
10 = x/16
10 * 16 = x
160 ounces = x
so 10 pounds is equivalent to 160 ounces. But we are not done yet.
We were asked to convert 10 pounds and 12 ounces.
So add together the ounces to find the total ounces:
160 ounces + 12 ounces = 172 ounces.
Help me please T^T
Solve for m.
m+1/3<-2 1/4

Answers
Answer:
B
Step-by-step explanation:
subtract 1/3 from both sides
m< -2 7/12
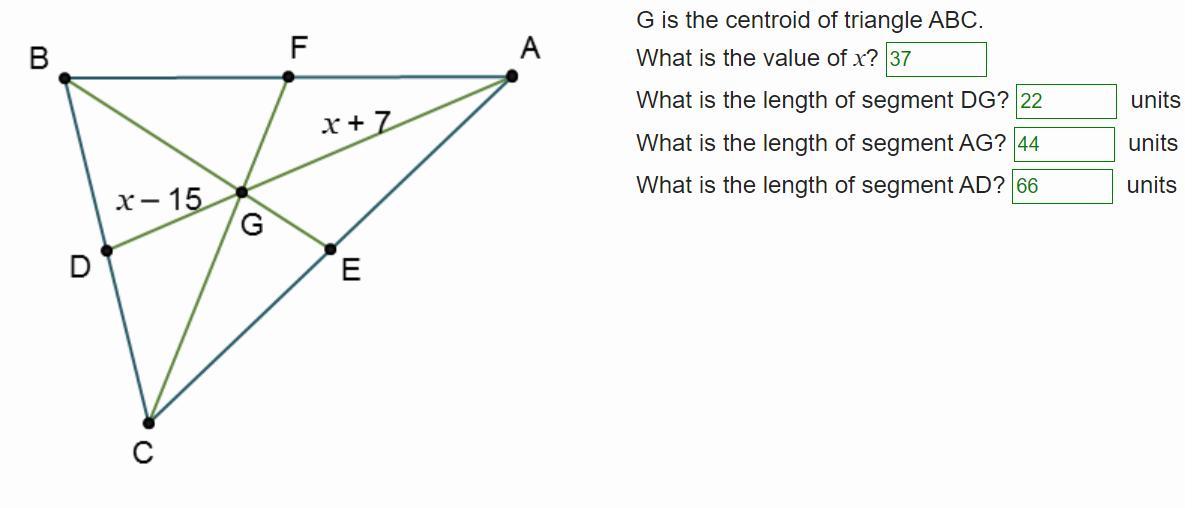
G is the centroid of triangle ABC.
What is the value of x?
22
What is the length of segment DG?
units
What is the length of segment AG?
units
What is the length of segment AD?
unit
Answers
Applying the centroid ratio theorem, we have:
x = 37
DG = 22
AG = 44
AD = 66.
What is the Centroid Ratio Theorem?According to the centroid ratio theorem, we have:
AG = 2/3(AD)
AG = x + 7
DG = x - 15
AD = x + 7 + x - 15 = 2x - 8
Plug in the values into the equation
x + 7 = 2/3(2x - 8)
3(x + 7) = 2(2x - 8)
3x + 21 = 4x - 16
3x - 4x = -21 - 16
-x = -37
x = 37
DG = x - 15 = 37 - 15 = 22
AG = x + 7 = 37 + 7 = 44
AD = 22 + 44 = 66
Learn more about the centroid ratio theorem on:
https://brainly.com/question/20627009
#SPJ1

Answer:
The value of x is 37
The length of segment DG is 22 units
The length of segment AG is 44 units
The length of segment AD is 66 units
Ali, Basti and Cian stand at three points A, B and C respectively. Suppose that the measure of angle ABC is 50 degrees , the measure of angle BAC is 60 degrees and Ali is exactly 150 ft away from Basti. Find the distance between Basti and Cian.

Answers
The distance between Basti and Cian is approximately 138.2 ft. Option D
To find the distance between Basti and Cian, we can use the Law of Sines, which relates the lengths of sides to the sines of their opposite angles in a triangle.
Let's label the points: A, B, and C. Ali is at point A, Basti is at point B, and Cian is at point C.
Given:
Angle ABC = 50 degrees (angle opposite side AC)
Angle BAC = 60 degrees (angle opposite side BC)
Ali is 150 ft away from Basti (side AB)
We want to find the distance between Basti and Cian, which is side BC.
Using the Law of Sines, we have:
BC/sin(50) = AB/sin(60)
Substituting the known values:
BC/sin(50) = 150/sin(60)
To find BC, we can rearrange the equation:
BC = (150/sin(60)) * sin(50)
Using a calculator to evaluate the expression:
BC ≈ 138.2 ft
Option D is correct.
For more such questions on distance visit:
https://brainly.com/question/30395212
#SPJ8
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
Write the expression in simplest form.
(-+ 3) - 2 (-x) =
Answers
Answer:
Simplest form of expression:
-3+2x
Answer:
2x - 3 (or) -3 + 2x
Step-by-step explanation:
Given equation,
→ (-+ 3) - 2 (-x)
The simplest form will be,
→ (-+ 3) - 2 (-x)
→ -3 + (-2 × -x)
→ -3 + 2x
→ 2x - 3
Thus, the answer is 2x - 3.
Rewrite in simplest terms: -8(-2a+4a-8)-7a
Answers
Answer:
-23a + 64
Step-by-step explanation:
-8(-2a + 4a - 8) - 7a
First combine like terms
-8(2a - 8) - 7a
Then distribute
-16a + 64 -7a
Combine like terms
-23a + 64
Find the equation of a line perpendicular to x=−5 that contains the point (3,−2).
Answers
the equation of the line perpendicular to x = -5 that contains the point (3, -2) is simply y = -2.
The equation x = -5 represents a vertical line passing through the point (-5, y) for any value of y. Any line perpendicular to this line must be a horizontal line passing through the point (x, -2), where x is a constant.
Thus, the equation of the line we are looking for is y = -2, since it is the equation of the horizontal line passing through the point (x, -2) for any value of x.
Therefore, the equation of the line perpendicular to x = -5 that contains the point (3, -2) is simply y = -2.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ1
Multiply the following using the vertical multiplication method:
x2 + 5x +1
x3x2 - 2x +4
O
A. 3x4 - 13x3 +3x2 + 18x + 4
B. 3x4 - x2 + 3x2 + x + 4
o
C. 3x4 + x2 + x2 +18x + 4
o
D. 3x4 +13x3 - 3x2 + 18x + 4
Answers
Answer:
a I think I might be a try it tell me if I am wrong
I don’t understand this

Answers
Answer:
144
Step-by-step explanation:
Answer:
This is the number of degrees Fahrenheit.
Step-by-step explanation:
For example, the 140 means 140 degrees. So, count the number of lines above 140... you'll see two more lines above, so the temp. is 142 degrees Fahrenheit.
Unless the lines mean a certain number. Such as 'each line means five'.
Do the directions mention an amount per line? If so, tell me in the comments. I cannot help if I don't know!
:)
Find u. See image below.

Answers
The value of u is 2 in the given right-angled triangle.
The given figure is a right-angled triangle with hypotenuse 'u' and the other two sides as \(\sqrt{2}\) and v.
We have to find the value of 'u' using Pythagoras theorem or trigonometric identities.
What is Pythagoras theorem?It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In a right-angled triangle ABC, if
BC = hypotenuse
AC and AB are the other two sides then,
\(BC^2 = AC^2 + AB^2\).
For this problem, we can find the value of u by using trigonometric identities.
From the figure, we have an angle of 45°.
Consider Cos 45°.
Cos Ф = base / hypotenuse
Cos 45° = \(\sqrt{2}\) / u ...........(1)
From trigonometric identities of cosine.
We have,
Cos 45° = 1 / \(\sqrt{2}\)............(2)
From (1) and (2)
We get,
1 / \(\sqrt{2}\) = \(\sqrt{2}\) / u
u = 2.
Thus the value of u is 2 in the given right-angled triangle.
Learn more about Pythagoras's theorem application here:
https://brainly.com/question/11687813
#SPJ1
if f(x)=x+2/x^2-9 and g(x)=11/x^2+3x
A. find f(x)+g(x)
B. list all of the excluded values
C. classify each type of discontinuty
To receive credit, this must be done by Algebraic methods, not graphing
Answers
The types of discontinuities are: removable discontinuity at x = -3 and vertical asymptotes at x = 0 and x = 3.
A. To find f(x) + g(x), we add the two functions together:
f(x) + g(x) = (x + 2)/(x^2 - 9) + 11/(x^2 + 3x)
To add these fractions, we need a common denominator. The common denominator in this case is (x^2 - 9)(x^2 + 3x). So, we rewrite the fractions with the common denominator:
f(x) + g(x) = [(x + 2)(x^2 + 3x) + 11(x^2 - 9)] / [(x^2 - 9)(x^2 + 3x)]
Simplifying the numerator:
f(x) + g(x) = (x^3 + 3x^2 + 2x^2 + 6x + 11x^2 - 99) / [(x^2 - 9)(x^2 + 3x)]
Combining like terms:
f(x) + g(x) = (x^3 + 16x^2 + 6x - 99) / [(x^2 - 9)(x^2 + 3x)]
B. To find the excluded values, we look for values of x that would make the denominators zero, as division by zero is undefined. In this case, the excluded values occur when:
(x^2 - 9) = 0 --> x = -3, 3
(x^2 + 3x) = 0 --> x = 0, -3
So, the excluded values are x = -3, 0, and 3.
C. To classify each type of discontinuity, we examine the excluded values and the behavior of the function around these points.
At x = -3, we have a removable discontinuity or hole since the denominator approaches zero but the numerator doesn't. The function can be simplified and defined at this point.
At x = 0 and x = 3, we have vertical asymptotes. The function approaches positive or negative infinity as x approaches these points, indicating a vertical asymptote.
Therefore, the types of discontinuities are: removable discontinuity at x = -3 and vertical asymptotes at x = 0 and x = 3.
For more questions on vertical .
https://brainly.com/question/30195815
#SPJ8
HELP PLZ PLZ HEEEEEEEEEEEEEEEEELP

Answers
Since there is 8 parts in between 1 and 2 on the number line the denominator is 8.
The most frequent measurement is right in the middle, which if you count to that line you can see it goes up to 4 parts.
And because it’s already past the whole number 1 it would be 1 4/8 or 1 ½
I hope this helps and is understandable!
Ashburn Company issued 15-year bonds two years ago at a coupon rate of 8.9 percent. The bonds make semiannual payments. If these bonds currently sell for 113 percent of par value, what is the YTM?
Answers
Using an online finance calculator, the yield to maturity (YTM) of the Ashburn Company's bond at a coupon rate of 8.9 percent paying semiannual interest and selling at 113% of par value is 7.45%.
What is the yield to maturity?The Yield to maturity (YTM) is the total return, expressed as an annual rate, anticipated by a bondholder on a bond if it is held until its maturity date.
The maturity date refers to the date when the principal of a fixed investment is repaid at the maturity value.
The yield to maturity can also be computed using the following formula:
YTM = [(Face value/Bond price)1/Time period]-1.
Face (par) value = $100
Bond current price = $113 ($100 x 113%)
Annual coupon rate = 8.9%
Coupon frequency = Semi-annually
Years to maturity = 15 years
Result:
Yield to maturity (YTM) = 7.45%
Learn more about the yield to maturity at https://brainly.com/question/457082.
#SPJ1
7 students are running for student council. how many different ways can their names be listed on the ballot
Answers
Step-by-step explanation:
7! = 5040 ways
Factor the expression below.
9x2 - 1
A. (x - 1)(9x + 1)
B. (3x - 1)(3x - 1)
C. (x - 1)(x-1)
D. (3x - 1)(3x + 1)
SUBMIT
Answers
Answer:
(3x -1) (3x+1)
Step-by-step explanation:
9x^2 - 1
Rewriting
(3x)^2 -1^2
This is the difference of squares a^2 -b^2 = (a+b) (a-b)
(3x -1) (3x+1)
The value of Factors of the expression are,
⇒ (3x - 1) (3x + 1)
We have to given that,
An expression for factor is,
⇒ 9x² - 1
We can use the formula for factor,
⇒ a² - b² = (a - b) (a + b)
So, We can factor it as,
⇒ 9x² - 1
⇒ (3x)² - 1²
⇒ (3x - 1) (3x + 1)
(By using above formula.)
Therefore, Factors of the expression are,
⇒ (3x - 1) (3x + 1)
Learn more about the equation visit:
brainly.com/question/28871326
#SPJ6
20 as a product of primes.
Use index notation when giving your answer
Answers
use a factor tree to get 2x2x5
2²x5
\(\huge\underline{\boxed{\bold{Hello\;there!}}}\)
20 as a product of primes:
2×2×5
Remember, primes have only two factors.
2 is only divisible by 1 and itself, and it's the only even prime number.
5 is also divisible by 1 and itself.
If we multiply 2 times 2 times 5, we will get 20.
\(\huge\boxed{\mathfrak{Answer:{\boxed{\boxed{2*2*5}}}}}\)
\(\bigstar\) I really hope it helps you!
\(\bold{Have\;a\;wonderful\;day!}\)
\(\rm{FabulousKingdom :-)\)
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.